Question

【題目】設等差數列{an}的公差為d，點（an ， bn）在函數f（x）=2x的圖象上（n∈N*）．
（1）若a1=﹣2，點（a8 ， 4b7）在函數f（x）的圖象上，求數列{an}的前n項和Sn；
（2）若a1=1，函數f（x）的圖象在點（a2 ， b2）處的切線在x軸上的截距為2﹣ ，求數列{ }的前n項和Tn ．

Answer 1

【答案】
（1）解：∵點（an，bn）在函數f（x）=2x的圖象上，

∴ ，

又等差數列{an}的公差為d，

∴ = =2d，

∵點（a8，4b7）在函數f（x）的圖象上，

∴ =b8，

∴ =4=2d，解得d=2．

又a1=﹣2，∴Sn= =﹣2n+ =n2﹣3n

（2）解：由f（x）=2x，∴f′（x）=2xln2，

∴函數f（x）的圖象在點（a2，b2）處的切線方程為 ，

又 ，令y=0可得x= ，

∴ ，解得a2=2．

∴d=a2﹣a1=2﹣1=1．

∴an=a1+（n﹣1）d=1+（n﹣1）×1=n，

∴bn=2n．

∴ ．

∴Tn= +…+ + ，

∴2Tn=1+ + +…+ ，

兩式相減得Tn=1+ +…+ ﹣ = ﹣

=

= ．

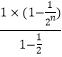【解析】（1）由于點（an ， bn）在函數f（x）=2x的圖象上，可得 ，又等差數列{an}的公差為d，利用等差數列的通項公式可得 =2d ． 由于點（a8 ， 4b7）在函數f（x）的圖象上，可得 =b8 ， 進而得到 =4=2d ， 解得d．再利用等差數列的前n項和公式即可得出．（2）利用導數的幾何意義可得函數f（x）的圖象在點（a2 ， b2）處的切線方程，即可解得a2 ． 進而得到an ， bn ． 再利用“錯位相減法”即可得出．
【考點精析】掌握數列的前n項和是解答本題的根本，需要知道數列{an}的前n項和sn與通項an的關系．