
【題目】已知函數(shù)![]() .
.
(1)若曲線![]() 在點(diǎn)
在點(diǎn)![]() 處的切線
處的切線![]() 與直線
與直線![]() 垂直,求實(shí)數(shù)
垂直,求實(shí)數(shù)![]() 的值;
的值;
(2)若![]() 恒成立,求實(shí)數(shù)
恒成立,求實(shí)數(shù)![]() 的取值范圍;
的取值范圍;
(3)證明:![]()
【答案】(1)![]() (2)
(2)![]() (3)證明見解析
(3)證明見解析
【解析】
試題(1)利用導(dǎo)數(shù)的幾何意義求曲線在點(diǎn)![]() 處的切線方程,注意這個點(diǎn)的切點(diǎn);
處的切線方程,注意這個點(diǎn)的切點(diǎn);
(2)對于恒成立的問題,常用到以下兩個結(jié)論:![]() 恒成立
恒成立![]() ,
,![]() 恒成立
恒成立![]() ;
;
(3)證明不等式,注意應(yīng)用前幾問的結(jié)論.
試題解析:(1)函數(shù)的定義域?yàn)?/span>![]() ,
,![]()
所以![]() ,又切線
,又切線![]() 與直線
與直線![]() 垂直,
垂直,
所以切線![]() 斜率為
斜率為![]() ,從而
,從而![]() ,解得
,解得![]() ,
,
(2)若![]() ,則
,則![]() 則
則![]() 在
在![]() 上是增函數(shù)
上是增函數(shù)
而![]() 不成立,故
不成立,故![]()
若![]() ,則當(dāng)
,則當(dāng)![]() 時,
時,![]() ;
;
當(dāng)![]() 時,
時,![]()
所以![]() 在
在![]() 上是增函數(shù),在
上是增函數(shù),在![]() 上是減函數(shù),
上是減函數(shù),
所以![]() 的最大值為
的最大值為![]()
要使![]() 恒成立,只需
恒成立,只需![]() ,解得
,解得![]()
(3)由(2)知,當(dāng)![]() 時,有
時,有![]() 在
在![]() 上恒成立,
上恒成立,
且![]() 在
在![]() 上是增函數(shù),
上是增函數(shù),
![]() 所以
所以![]() 在
在![]() 上恒成立 .
上恒成立 .
令![]() ,則
,則![]()
令![]() 則有
則有
![]()
以上各式兩邊分別相加,
得![]()
即![]()
故![]()


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學(xué)生10分鐘應(yīng)用題系列答案
小學(xué)生10分鐘應(yīng)用題系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() 定義域?yàn)?/span>
定義域?yàn)?/span>![]() ,設(shè)
,設(shè)![]() .
.
(1)試確定![]() 的取值范圍,使得函數(shù)
的取值范圍,使得函數(shù)![]() 在
在![]() 上為單調(diào)函數(shù);
上為單調(diào)函數(shù);
(2)求證:![]() ;
;
(3)求證:對于任意的![]() ,總存在
,總存在![]() ,滿足
,滿足![]() ,并確定這樣的
,并確定這樣的![]() 的個數(shù).
的個數(shù).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在全面抗擊新冠肺炎疫情這一特殊時期,我市教育局提出“停課不停學(xué)”的口號,鼓勵學(xué)生線上學(xué)習(xí).某校數(shù)學(xué)教師為了調(diào)查高三學(xué)生數(shù)學(xué)成績與線上學(xué)習(xí)時間之間的相關(guān)關(guān)系,對高三年級隨機(jī)選取45名學(xué)生進(jìn)行跟蹤問卷,其中每周線上學(xué)習(xí)數(shù)學(xué)時間不少于5小時的有19人,余下的人中,在檢測考試中數(shù)學(xué)平均成績不足120分的占![]() ,統(tǒng)計成績后得到如下
,統(tǒng)計成績后得到如下![]() 列聯(lián)表:
列聯(lián)表:
分?jǐn)?shù)不少于120分 | 分?jǐn)?shù)不足120分 | 合計 | |
線上學(xué)習(xí)時間不少于5小時 | 4 | 19 | |
線上學(xué)習(xí)時間不足5小時 | |||
合計 | 45 |
(1)請完成上面![]() 列聯(lián)表;并判斷是否有99%的把握認(rèn)為“高三學(xué)生的數(shù)學(xué)成績與學(xué)生線上學(xué)習(xí)時間有關(guān)”;
列聯(lián)表;并判斷是否有99%的把握認(rèn)為“高三學(xué)生的數(shù)學(xué)成績與學(xué)生線上學(xué)習(xí)時間有關(guān)”;
(2)在上述樣本中從分?jǐn)?shù)不少于120分的學(xué)生中,按照分層抽樣的方法,抽到線上學(xué)習(xí)時間不少于5小時和線上學(xué)習(xí)時間不足5小時的學(xué)生共5名,若在這5名學(xué)生中隨機(jī)抽取2人,求至少1人每周線上學(xué)習(xí)時間不足5小時的概率.
(下面的臨界值表供參考)
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(參考公式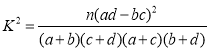 其中
其中![]() )
)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如果函數(shù)![]() 的導(dǎo)函數(shù)
的導(dǎo)函數(shù)![]() 的圖象如圖所示,則以下關(guān)于函數(shù)
的圖象如圖所示,則以下關(guān)于函數(shù)![]() 的判斷:
的判斷:
①在區(qū)間![]() 內(nèi)單調(diào)遞增;
內(nèi)單調(diào)遞增;
②在區(qū)間![]() 內(nèi)單調(diào)遞減;
內(nèi)單調(diào)遞減;
③在區(qū)間![]() 內(nèi)單調(diào)遞增;
內(nèi)單調(diào)遞增;
④![]() 是極小值點(diǎn);
是極小值點(diǎn);
⑤![]() 是極大值點(diǎn).
是極大值點(diǎn).
其中正確的是( )
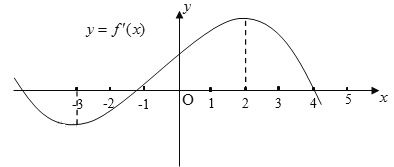
A. ③⑤B. ②③C. ①④⑤D. ①②④
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】3月3日,武漢大學(xué)人民醫(yī)院的團(tuán)隊(duì)在預(yù)印本平臺![]() 上發(fā)布了一項(xiàng)研究:在新冠肺炎病例的統(tǒng)計數(shù)據(jù)中,男性患者往往比女性患者多.研究者分析了1月1日~29日的6013份病例數(shù)據(jù),發(fā)現(xiàn)
上發(fā)布了一項(xiàng)研究:在新冠肺炎病例的統(tǒng)計數(shù)據(jù)中,男性患者往往比女性患者多.研究者分析了1月1日~29日的6013份病例數(shù)據(jù),發(fā)現(xiàn)![]() 的患者為男性;進(jìn)入重癥監(jiān)護(hù)病房的患者中,則有
的患者為男性;進(jìn)入重癥監(jiān)護(hù)病房的患者中,則有![]() 為男性.隨后,他們分析了武漢大學(xué)人民醫(yī)院的數(shù)據(jù).他們按照癥狀程度的不同進(jìn)行分析,結(jié)果發(fā)現(xiàn),男性患者有
為男性.隨后,他們分析了武漢大學(xué)人民醫(yī)院的數(shù)據(jù).他們按照癥狀程度的不同進(jìn)行分析,結(jié)果發(fā)現(xiàn),男性患者有![]() 為危重,而女性患者危重情況的為
為危重,而女性患者危重情況的為![]() .也就是說男性的發(fā)病情況似乎普遍更嚴(yán)重.研究者總結(jié)道:“男性在新冠肺炎的傳播中扮演著重要的角色.”那么,病毒真的偏愛男性嗎?有一個中學(xué)生學(xué)習(xí)小組,在自己封閉的社區(qū)進(jìn)行無接觸抽樣問卷調(diào)查,收集到男、女患者各50個數(shù)據(jù),統(tǒng)計如下:
.也就是說男性的發(fā)病情況似乎普遍更嚴(yán)重.研究者總結(jié)道:“男性在新冠肺炎的傳播中扮演著重要的角色.”那么,病毒真的偏愛男性嗎?有一個中學(xué)生學(xué)習(xí)小組,在自己封閉的社區(qū)進(jìn)行無接觸抽樣問卷調(diào)查,收集到男、女患者各50個數(shù)據(jù),統(tǒng)計如下:
輕—中度感染 | 重度(包括危重) | 總計 | |
男性患者 |
|
|
|
女性患者 |
|
|
|
總計 |
|
|
|
(1)求![]() 列聯(lián)表中的數(shù)據(jù)
列聯(lián)表中的數(shù)據(jù)![]() 的值;
的值;
(2)能否有![]() 把握認(rèn)為,新冠肺炎的感染程度和性別有關(guān)?
把握認(rèn)為,新冠肺炎的感染程度和性別有關(guān)?
(3)該學(xué)生實(shí)驗(yàn)小組打算從“輕—中度感染”的患者中按男女比例再抽取5人,追蹤某種中藥制劑的效果.然后從這5人中隨機(jī)抽取3人進(jìn)行每日的健康記錄,求至少抽到2名女性患者的概率.
附表及公式:![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() ,若關(guān)于
,若關(guān)于![]() 的方程
的方程![]() 恰有兩個不相等的實(shí)數(shù)根, 則實(shí)數(shù)
恰有兩個不相等的實(shí)數(shù)根, 則實(shí)數(shù)![]() 的取值范圍是
的取值范圍是![]()
![]()
A. ![]() B.
B. ![]() ,
,![]() C.
C. ![]() ,
,![]() D.
D. ![]() ,
,![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() ,其中a∈R.
,其中a∈R.
(Ⅰ)討論函數(shù)![]() 的單調(diào)性;
的單調(diào)性;
(Ⅱ)當(dāng)![]() 時,設(shè)
時,設(shè)![]() 、
、![]() 為曲線
為曲線![]() 上任意兩點(diǎn),曲線
上任意兩點(diǎn),曲線![]() 在點(diǎn)
在點(diǎn)![]() 處的切線斜率為k,證明:
處的切線斜率為k,證明:![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】選修4-4:坐標(biāo)系與參數(shù)方程
在直角坐標(biāo)系![]() 中,直線
中,直線![]() 的方程為
的方程為![]() ,曲線
,曲線![]() :
:![]() (
(![]() 為參數(shù),
為參數(shù),![]() ),在以原點(diǎn)
),在以原點(diǎn)![]() 為極點(diǎn),
為極點(diǎn),![]() 軸正半軸為極軸的極坐標(biāo)系中,曲線
軸正半軸為極軸的極坐標(biāo)系中,曲線![]() :
:![]() .
.
(1)求曲線![]() 的普通方程和曲線
的普通方程和曲線![]() 的直角坐標(biāo)方程;
的直角坐標(biāo)方程;
(2)若直線![]() 與曲線
與曲線![]() 有公共點(diǎn),且直線
有公共點(diǎn),且直線![]() 與曲線
與曲線![]() 的交點(diǎn)
的交點(diǎn)![]() 恰好在曲線
恰好在曲線![]() 與
與![]() 軸圍成的區(qū)域(不含邊界)內(nèi),求
軸圍成的區(qū)域(不含邊界)內(nèi),求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com