Question

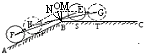
【題目】某種型號汽車四個輪胎半徑相同，均為R=40cm，同側前后兩輪胎之間的距離（指輪胎中心之間距離）為l=280cm （假定四個輪胎中心構成一個矩形）．當該型號汽車開上一段上坡路ABC（如圖（1）所示，其中∠ABC=a（ ），且前輪E已在BC段上時，后輪中心在F位置；若前輪中心到達G處時，后輪中心在H處（假定該汽車能順利駛上該上坡路）．設前輪中心在E和G處時與地面的接觸點分別為S和T，且BS=60cm，ST=100cm．（其它因素忽略不計）

（1）如圖（2）所示，FH和GE的延長線交于點O，求證：OE=40cot （cm）；
（2）當a= π時，后輪中心從F處移動到H處實際移動了多少厘米？（精確到1cm）

Answer 1

【答案】
（1）解：由OE∥BC，OH∥AB，得∠EOH=α，

過點B作BM⊥OE，BN⊥OH，則

Rt△OMB Rt△ONB，從而∠BOM= ．

在Rt△OMB中，由BM=40得OM=40cot ，從而，OE=OM+ME=OM+BS=40cot +60

（2）解：由（1）結論得OE= +60．

設OH=x，OF=y，在△OHG中，由余弦定理得，

2802=x2+（ +60+100）2﹣2x（ +60+100）cos150°，

解得x≈118.8cm．）

在△OEF中，由余弦定理得，

2802=y2+（ +60）2﹣2y（ +60）cos150°，

解得y≈216.5cm．）

所以，FH=y﹣x≈98cm，

即后輪中心從F處移動到H處實際移動了約98cm．

【解析】（1）依題意，∠EOH=α，由Rt△OMB Rt△ONB，可求得∠BOM= ，在Rt△OMB中，可求得OM=40cot ，從而可證得結論；（2）由（1）結論得OE= +60，設OH=x，OF=y，在△OHG中，由余弦定理可求得x，在△OEF中，由余弦定理可求得y，而FH=y﹣x，從而可得答案．
【考點精析】本題主要考查了余弦定理的定義的相關知識點，需要掌握余弦定理:;;才能正確解答此題．