
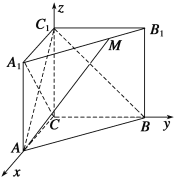
【題目】如圖所示,在直三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,點
,點![]() 在線段
在線段![]() 上.
上.
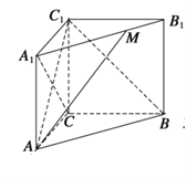
(1)若![]() ,求異面直線
,求異面直線![]() 和
和![]() 所成角的余弦值;
所成角的余弦值;
(2)若直線![]() 與平面
與平面![]() 所成角為
所成角為![]() ,試確定點
,試確定點![]() 的位置.
的位置.
【答案】(1)![]() (2)點M是線段
(2)點M是線段![]() 的中點.
的中點.
【解析】
(1)以![]() 為坐標原點,分別以
為坐標原點,分別以![]() ,
,![]() ,
,![]() 所在直線為
所在直線為![]() 軸,
軸,![]() 軸,
軸,![]() 軸,建立如圖所示的空間直角坐標系,得到
軸,建立如圖所示的空間直角坐標系,得到![]() ,
,![]() ,再代入向量夾角公式計算,即可得答案;
,再代入向量夾角公式計算,即可得答案;
(2)設![]() ,得
,得![]() ,直線
,直線![]() 與平面
與平面![]() 所成角為
所成角為![]() ,得到關于
,得到關于![]() 的方程,解方程即可得到點
的方程,解方程即可得到點![]() 的位置.
的位置.
以![]() 為坐標原點,分別以
為坐標原點,分別以![]() ,
,![]() ,
,![]() 所在直線為
所在直線為![]() 軸,
軸,![]() 軸,
軸,![]() 軸,建立如圖所示的空間直角坐標系,則
軸,建立如圖所示的空間直角坐標系,則![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)因為![]() ,所以
,所以![]() .
.
所以![]() ,
,![]() .
.
所以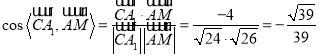 .
.
所以異面直線![]() 和
和![]() 所成角的余弦值為
所成角的余弦值為![]() .
.
(2)由![]() ,
,![]() ,
,![]() ,
,
知![]() ,
,![]() .
.
設平面![]() 的法向量為
的法向量為![]() ,由
,由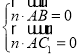 得
得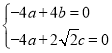 ,
,
令![]() ,則
,則![]() ,
,![]() ,所以平面
,所以平面![]() 的一個法向量為
的一個法向量為![]() .
.
因為點![]() 在線段
在線段![]() 上,所以可設
上,所以可設![]() ,所以
,所以![]() ,
,
因為直線![]() 與平面
與平面![]() 所成角為
所成角為![]() ,所以
,所以![]() .
.
由![]() ,得
,得![]() ,
,
解得![]() 或
或![]() .
.
因為點![]() 在線段
在線段![]() 上,所以
上,所以![]() ,
,
即點![]() 是線段
是線段![]() 的中點.
的中點.


科目:高中數學 來源: 題型:
【題目】2019年,河南省鄭州市的房價依舊是鄭州市民關心的話題.總體來說,二手房房價有所下降,相比二手房而言,新房市場依然強勁,價格持續升高.已知銷售人員主要靠售房提成領取工資.現統計鄭州市某新房銷售人員一年的工資情況的結果如圖所示,若近幾年來該銷售人員每年的工資總體情況基本穩定,則下列說法正確的是( )

A.月工資增長率最高的為8月份
B.該銷售人員一年有6個月的工資超過4000元
C.由此圖可以估計,該銷售人員2020年6,7,8月的平均工資將會超過5000元
D.該銷售人員這一年中的最低月工資為1900元
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四邊形![]() 中,
中,![]() ,以
,以![]() 為折痕把
為折痕把![]() 折起,使點
折起,使點![]() 到達點
到達點![]() 的位置,且
的位置,且![]() .
.
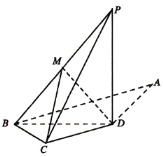
(1)證明:![]() 平面
平面![]() ;
;
(2)若![]() 為
為![]() 的中點,二面角
的中點,二面角![]() 等于60°,求直線
等于60°,求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校周五的課程表設計中,要求安排8節課(上午4節下午4節),分別安排語文數學英語物理化學生物政治歷史各一節,其中生物只能安排在第一節或最后一節,數學和英語在安排時必須相鄰(注:上午的最后一節與下午的第一節不記作相鄰),則周五的課程順序的編排方法共有( ).
A.4800種B.2400種C.1200種D.240種
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,一條東西流向的筆直河流,現利用航拍無人機![]() 監控河流南岸相距150米的
監控河流南岸相距150米的![]()
![]() 兩點處(
兩點處(![]() 在
在![]() 的正西方向),河流北岸的監控中心
的正西方向),河流北岸的監控中心![]() 在
在![]() 的正北方100米處,監控控制車
的正北方100米處,監控控制車![]() 在
在![]() 的正西方向,且在通向
的正西方向,且在通向![]() 的沿河路上運動,監控過程中,保證監控控制車
的沿河路上運動,監控過程中,保證監控控制車![]() 到無人機
到無人機![]() 和到監控中心
和到監控中心![]() 的距離之和150米,平面
的距離之和150米,平面![]() 始終垂直于水平面
始終垂直于水平面![]() ,且
,且![]() ,
,![]()
![]() 兩點間距離維持在100米.
兩點間距離維持在100米.
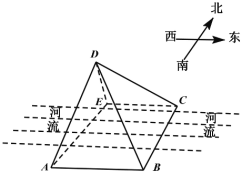
(1)當監控控制車![]() 到監控中心
到監控中心![]() 的距離為100米時,求無人機
的距離為100米時,求無人機![]() 距離水平面
距離水平面![]() 的距離;
的距離;
(2)若記無人機![]() 看
看![]() 處的俯角(
處的俯角(![]() ),監控過程中,四棱錐
),監控過程中,四棱錐![]() 內部區域的體積為監控影響區域
內部區域的體積為監控影響區域![]() ,請將
,請將![]() 表示為關于
表示為關于![]() 的函數,并求出監控影響區域的最大值.
的函數,并求出監控影響區域的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】數學中有許多形狀優美寓意美好的曲線,曲線![]() 就是其中之一(如圖).給出下列三個結論:
就是其中之一(如圖).給出下列三個結論:

①曲線![]() 恰好經過6個整點(即橫縱坐標均為整數的點);
恰好經過6個整點(即橫縱坐標均為整數的點);
②曲線![]() 上存在到原點的距離超過
上存在到原點的距離超過![]() 的點;
的點;
③曲線![]() 所圍成的“心形”區域的面積小于3.
所圍成的“心形”區域的面積小于3.
其中,所有錯誤結論的序號是______.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 在點
在點![]() 處的切線方程為
處的切線方程為![]() .
.
(1)求![]() ,
,![]() ;
;
(2)函數![]() 圖像與
圖像與![]() 軸負半軸的交點為
軸負半軸的交點為![]() ,且在點
,且在點![]() 處的切線方程為
處的切線方程為![]() ,函數
,函數![]() ,
,![]() ,求
,求![]() 的最小值;
的最小值;
(3)關于![]() 的方程
的方程![]() 有兩個實數根
有兩個實數根![]() ,
,![]() ,且
,且![]() ,證明:
,證明:![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com