
【題目】設(shè)函數(shù)![]() .
.
(1)當(dāng)b=0時(shí),求函數(shù)![]() 的極小值;
的極小值;
(2)若已知b>1且函數(shù)![]() 與直線y=-x相切,求b的值;
與直線y=-x相切,求b的值;
(3)在(2)的條件下,函數(shù)![]() 與直線y=-x+m有三個(gè)公共點(diǎn),求m的取值范圍.(直接寫出答案)
與直線y=-x+m有三個(gè)公共點(diǎn),求m的取值范圍.(直接寫出答案)
【答案】(1)![]() (2)b=3(3)
(2)b=3(3)![]()
【解析】
(1)求導(dǎo)得到函數(shù)的單調(diào)區(qū)間,再計(jì)算極小值.
(2)設(shè)切點(diǎn)是(![]() ),求導(dǎo),根據(jù)條件得到
),求導(dǎo),根據(jù)條件得到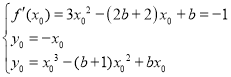 計(jì)算得到答案.
計(jì)算得到答案.
(3)化簡(jiǎn)得到![]() ,設(shè)
,設(shè)![]() ,畫出函數(shù)圖象得到答案.
,畫出函數(shù)圖象得到答案.
(1)當(dāng)b=0時(shí),![]() 則
則![]() ,由
,由![]() 得
得![]() ,
,
當(dāng)![]() 或
或![]() 時(shí),
時(shí),![]() ;當(dāng)
;當(dāng)![]() 時(shí),
時(shí),![]() ,
,
則當(dāng)![]() 時(shí),f(x)取得極小值
時(shí),f(x)取得極小值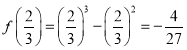
(2)因![]() ,則
,則![]()
設(shè)函數(shù)![]() 與直線y=-x相切的切點(diǎn)是(
與直線y=-x相切的切點(diǎn)是(![]() ),
),
因?yàn)?/span>![]() ,所以
,所以![]() ,
,
所以有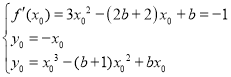
又![]() ,相減得
,相減得![]() ,
,
所以![]() ,所以
,所以![]() ,解得b=3.
,解得b=3.
(3)![]()
設(shè)![]() ,
,![]()
![]() 在
在![]() 上單調(diào)遞增;在
上單調(diào)遞增;在![]() 單調(diào)遞減.
單調(diào)遞減.
極大值![]() ,極小值
,極小值![]() ,畫出函數(shù)圖象:
,畫出函數(shù)圖象:
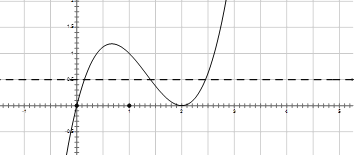
根據(jù)圖象得到答案:![]() .
.


 閱讀快車系列答案
閱讀快車系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】上海途安型號(hào)出租車價(jià)格規(guī)定:起步費(fèi)![]() 元,可行
元,可行![]() 千米;
千米;![]() 千米以后按每千米按
千米以后按每千米按![]() 元計(jì)價(jià),可再行
元計(jì)價(jià),可再行![]() 千米;以后每千米都按
千米;以后每千米都按![]() 元計(jì)價(jià)。假如忽略因交通擁擠而等待的時(shí)間.
元計(jì)價(jià)。假如忽略因交通擁擠而等待的時(shí)間.
![]() 請(qǐng)建立車費(fèi)
請(qǐng)建立車費(fèi)![]() (元)和行車?yán)锍?/span>
(元)和行車?yán)锍?/span>![]() (千米)之間的函數(shù)關(guān)系式;
(千米)之間的函數(shù)關(guān)系式;
![]() 注意到上海出租車的計(jì)價(jià)系統(tǒng)是以元為單位計(jì)價(jià)的,如:小明乘坐途安型號(hào)出租車從華師大二附中本部到浦東實(shí)驗(yàn)學(xué)校走路線一(路線一總長(zhǎng)
注意到上海出租車的計(jì)價(jià)系統(tǒng)是以元為單位計(jì)價(jià)的,如:小明乘坐途安型號(hào)出租車從華師大二附中本部到浦東實(shí)驗(yàn)學(xué)校走路線一(路線一總長(zhǎng)![]() 千米)須付車費(fèi)
千米)須付車費(fèi)![]() 元,走路線二(路線二總長(zhǎng)
元,走路線二(路線二總長(zhǎng)![]() 千米)也須付車費(fèi)
千米)也須付車費(fèi)![]() 元.將上述函數(shù)解析式進(jìn)行修正(符號(hào)
元.將上述函數(shù)解析式進(jìn)行修正(符號(hào)![]() 表示不大于
表示不大于![]() 的最大整數(shù),符號(hào)
的最大整數(shù),符號(hào)![]() 表示不小于
表示不小于![]() 的最小整數(shù));并求小明乘坐途安型號(hào)出租車從華師大二附中本部到閔行分校須付車費(fèi)多少元?(注:兩校區(qū)路線長(zhǎng)
的最小整數(shù));并求小明乘坐途安型號(hào)出租車從華師大二附中本部到閔行分校須付車費(fèi)多少元?(注:兩校區(qū)路線長(zhǎng)![]() 千米)
千米)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() 的左、右焦點(diǎn)為
的左、右焦點(diǎn)為![]() 、
、![]() .
.
(1)求以![]() 為焦點(diǎn),原點(diǎn)為頂點(diǎn)的拋物線方程;
為焦點(diǎn),原點(diǎn)為頂點(diǎn)的拋物線方程;
(2)若橢圓![]() 上點(diǎn)
上點(diǎn)![]() 滿足
滿足![]() ,求
,求![]() 的縱坐標(biāo)
的縱坐標(biāo)![]() ;
;
(3)設(shè)![]() ,若橢圓
,若橢圓![]() 上存在兩個(gè)不同點(diǎn)
上存在兩個(gè)不同點(diǎn)![]() 、
、![]() 滿足
滿足![]() ,證明:直線
,證明:直線![]() 過定點(diǎn),并求該定點(diǎn)的坐標(biāo).
過定點(diǎn),并求該定點(diǎn)的坐標(biāo).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知二次函數(shù)![]() 的圖象的頂點(diǎn)坐標(biāo)為
的圖象的頂點(diǎn)坐標(biāo)為![]() ,且過坐標(biāo)原點(diǎn)
,且過坐標(biāo)原點(diǎn)![]() .數(shù)列
.數(shù)列![]() 的前
的前![]() 項(xiàng)和為
項(xiàng)和為![]() ,點(diǎn)
,點(diǎn)![]() 在二次函數(shù)
在二次函數(shù)![]() 的圖象上.
的圖象上.
(Ⅰ)求數(shù)列![]() 的通項(xiàng)公式;
的通項(xiàng)公式;
(Ⅱ)設(shè)![]() ,數(shù)列
,數(shù)列![]() 的前
的前![]() 項(xiàng)和為
項(xiàng)和為![]() ,若
,若![]() 對(duì)
對(duì)![]() 恒成立,求實(shí)數(shù)
恒成立,求實(shí)數(shù)![]() 的取值范圍;
的取值范圍;
(Ⅲ)在數(shù)列![]() 中是否存在這樣一些項(xiàng):
中是否存在這樣一些項(xiàng):![]()
![]()
![]() ,這些項(xiàng)都能夠構(gòu)成以
,這些項(xiàng)都能夠構(gòu)成以![]() 為首項(xiàng),
為首項(xiàng),![]() 為公比的等比數(shù)列
為公比的等比數(shù)列![]() ?若存在,寫出
?若存在,寫出![]() 關(guān)于
關(guān)于![]() 的表達(dá)式;若不存在,說明理由.
的表達(dá)式;若不存在,說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
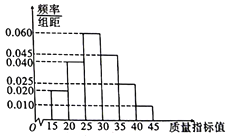
【題目】某企業(yè)為提高生產(chǎn)質(zhì)量,引入了一批新的生產(chǎn)設(shè)備,為了解生產(chǎn)情況,隨機(jī)抽取了新、舊設(shè)備生產(chǎn)的共200件產(chǎn)品進(jìn)行質(zhì)量檢測(cè),統(tǒng)計(jì)得到產(chǎn)品的質(zhì)量指標(biāo)值如下表及圖(所有產(chǎn)品質(zhì)量指標(biāo)值均位于區(qū)間![]() 內(nèi)),若質(zhì)量指標(biāo)值大于30,則說明該產(chǎn)品質(zhì)量高,否則說明該產(chǎn)品質(zhì)量一般.
內(nèi)),若質(zhì)量指標(biāo)值大于30,則說明該產(chǎn)品質(zhì)量高,否則說明該產(chǎn)品質(zhì)量一般.
質(zhì)量指標(biāo) | 頻數(shù) |
| 2 |
| 8 |
| 10 |
| 30 |
| 20 |
| 10 |
合計(jì) | 80 |
(1)根據(jù)上述圖表完成下列![]() 列聯(lián)表,并判斷是否有
列聯(lián)表,并判斷是否有![]() 的把握認(rèn)為產(chǎn)品質(zhì)量高與引人新設(shè)備有關(guān);
的把握認(rèn)為產(chǎn)品質(zhì)量高與引人新設(shè)備有關(guān);
新舊設(shè)備產(chǎn)品質(zhì)量![]() 列聯(lián)表
列聯(lián)表
產(chǎn)品質(zhì)量高 | 產(chǎn)品質(zhì)量一般 | 合計(jì) | |
新設(shè)備產(chǎn)品 | |||
舊設(shè)備產(chǎn)品 | |||
合計(jì) |
(2)從舊設(shè)備生產(chǎn)的質(zhì)量指標(biāo)值位于區(qū)間![]() 的產(chǎn)品中,按分層抽樣抽取6件產(chǎn)品,再?gòu)倪@6件產(chǎn)品中隨機(jī)選取2件產(chǎn)品進(jìn)行質(zhì)量檢測(cè),求至少有一件產(chǎn)品質(zhì)量指標(biāo)值位于
的產(chǎn)品中,按分層抽樣抽取6件產(chǎn)品,再?gòu)倪@6件產(chǎn)品中隨機(jī)選取2件產(chǎn)品進(jìn)行質(zhì)量檢測(cè),求至少有一件產(chǎn)品質(zhì)量指標(biāo)值位于![]() 的概率.
的概率.
附: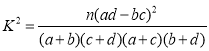 ,
,![]() .
.
| 0.10 | 0.05 | 0.01 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】舉行動(dòng)物運(yùn)動(dòng)會(huì)其中有小兔大兔接力賽跑一項(xiàng),跑道從起點(diǎn)![]() 經(jīng)過點(diǎn)
經(jīng)過點(diǎn)![]() 再到終點(diǎn)
再到終點(diǎn)![]() ,其中
,其中![]() 米,
米,![]() 米,規(guī)定小兔跑第一棒從
米,規(guī)定小兔跑第一棒從![]() 到
到![]() ,大兔在
,大兔在![]() 處接力完成跑第二棒從
處接力完成跑第二棒從![]() 到
到![]() ,假定接力賽跑時(shí)小兔大兔的各自速度都是均勻的,且它們的速度之和為定值10米/秒,試問小兔和大兔應(yīng)以怎樣的速度接力賽跑,才能使接力賽成績(jī)最好(所需時(shí)間最短),并求其最短時(shí)間.
,假定接力賽跑時(shí)小兔大兔的各自速度都是均勻的,且它們的速度之和為定值10米/秒,試問小兔和大兔應(yīng)以怎樣的速度接力賽跑,才能使接力賽成績(jī)最好(所需時(shí)間最短),并求其最短時(shí)間.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)若關(guān)于x的方程![]() 有解,求實(shí)數(shù)a的最小整數(shù)值;
有解,求實(shí)數(shù)a的最小整數(shù)值;
(2)若對(duì)任意的![]() ,函數(shù)
,函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上的最大值與最小值的差不超過1,求實(shí)數(shù)a的取值范圍.
上的最大值與最小值的差不超過1,求實(shí)數(shù)a的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() (
(![]() 是自然對(duì)數(shù)的底數(shù))
是自然對(duì)數(shù)的底數(shù))
(1)求證: ![]()
(2)若不等式![]() 在
在![]() 上恒成立,求正數(shù)
上恒成立,求正數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
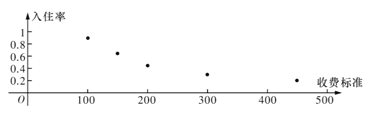
【題目】某創(chuàng)業(yè)者計(jì)劃在某旅游景區(qū)附近租賃一套農(nóng)房發(fā)展成特色“農(nóng)家樂”,為了確定未來發(fā)展方向此創(chuàng)業(yè)者對(duì)該景區(qū)附近五家“農(nóng)家樂”跟蹤調(diào)查了100天,這五家“農(nóng)家樂的收費(fèi)標(biāo)準(zhǔn)互不相同得到的統(tǒng)計(jì)數(shù)據(jù)如下表,x為收費(fèi)標(biāo)準(zhǔn)(單位:元/日),t為入住天數(shù)(單位:天),以頻率作為各自的“入住率”,收費(fèi)標(biāo)準(zhǔn)x與“入住率”y的散點(diǎn)圖如圖
x | 100 | 150 | 200 | 300 | 450 |
t | 90 | 65 | 45 | 30 | 20 |
(1)若從以上五家“農(nóng)家樂”中隨機(jī)抽取兩家深人調(diào)查,記![]() 為“入住率超過0.6的農(nóng)家樂的個(gè)數(shù),求
為“入住率超過0.6的農(nóng)家樂的個(gè)數(shù),求![]() 的概率分布列
的概率分布列
(2)z=lnx,由散點(diǎn)圖判斷![]() 與
與![]() 哪個(gè)更合適于此模型(給出判斷即可不必說明理由)?并根據(jù)你的判斷結(jié)果求回歸方程(a,
哪個(gè)更合適于此模型(給出判斷即可不必說明理由)?并根據(jù)你的判斷結(jié)果求回歸方程(a,![]() 的結(jié)果精確到0.1)
的結(jié)果精確到0.1)
(3)根據(jù)第(2)問所求的回歸方程,試估計(jì)收費(fèi)標(biāo)準(zhǔn)為多少時(shí),100天銷售額L最大?(100天銷售額L=100×入住率×收費(fèi)標(biāo)準(zhǔn)x)
參考數(shù)據(jù)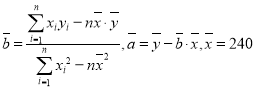 ,
,![]() ,
,![]()
![]()
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com