
【題目】已知拋物線E:y2=2px(p>0),焦點F到準線的距離為3,拋物線E上的兩個動點A(x1,y1)和B(x2,y2),其中x1≠x2且x1+x2=4.線段AB的垂直平分線與x軸交于點 C.
(1)求拋物線E的方程;
(2)求△ABC面積的最大值.
【答案】(1)y2=6x(2)![]() .
.
【解析】
(1)根據拋物線定義,寫出焦點坐標和準線方程,列方程即可得解;
(2)根據中點坐標表示出|AB|和點到直線的距離,得出面積,利用均值不等式求解最大值.
(1)拋物線E:y2=2px(p>0),焦點F(![]() ,0)到準線x
,0)到準線x![]() 的距離為3,可得p=3,即有拋物線方程為y2=6x;
的距離為3,可得p=3,即有拋物線方程為y2=6x;
(2)設線段AB的中點為M(x0,y0),則![]() ,
,
y0![]() ,kAB
,kAB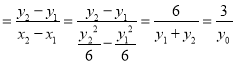 ,
,
則線段AB的垂直平分線方程為y﹣y0![]() (x﹣2),①
(x﹣2),①
可得x=5,y=0是①的一個解,所以AB的垂直平分線與x軸的交點C為定點,
且點C(5,0),由①可得直線AB的方程為y﹣y0![]() (x﹣2),即x
(x﹣2),即x![]() (y﹣y0)+2 ②
(y﹣y0)+2 ②
代入y2=6x可得y2=2y0(y﹣y0)+12,即y2﹣2y0y+2y02=0 ③,
由題意y1,y2是方程③的兩個實根,且y1≠y2,
所以△=4y02﹣4(2y02﹣12)=﹣4y02+48>0,解得﹣2![]() y0<2
y0<2![]() ,
,
|AB|![]()
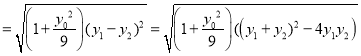
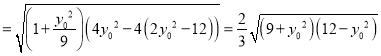 ,
,
又C(5,0)到線段AB的距離h=|CM|![]() ,
,
所以S△ABC![]()
![]()
![]()
![]() ,
,
當且僅當9+y02=24﹣2y02,即y0=±![]() ,A(
,A(![]() ,
,![]() ),B(
),B(![]() ,
,![]() ),
),
或A(![]() ,
,![]() ),B(
),B(![]() ,
,![]() )時等號成立,
)時等號成立,
所以S△ABC的最大值為![]() .
.


 培優口算題卡系列答案
培優口算題卡系列答案 開心口算題卡系列答案
開心口算題卡系列答案 口算題卡河北少年兒童出版社系列答案
口算題卡河北少年兒童出版社系列答案 A加金題 系列答案
A加金題 系列答案科目:高中數學 來源: 題型:
【題目】已知矩形EFMN,![]() ,
,![]() ,以EF的中點O為原點,建立如圖的平面直角坐標系,若橢圓
,以EF的中點O為原點,建立如圖的平面直角坐標系,若橢圓![]() 以E,F為焦點,且經過M,N兩點.
以E,F為焦點,且經過M,N兩點.
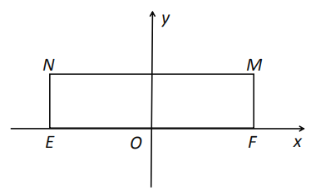
(1)求橢圓![]() 的方程;
的方程;
(2)直線![]() 與
與![]() 相交于A,B兩點,在y軸上是否存在點C,使得△ABC為正三角形,若存在,求出l的方程;若不存在,說明理由.
相交于A,B兩點,在y軸上是否存在點C,使得△ABC為正三角形,若存在,求出l的方程;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為方便市民出行,倡導低碳出行.某市公交公司推出利用支付寶和微信掃碼支付乘車活動,活動設置了一段時間的推廣期,在推廣期內采用隨機優惠鼓勵市民掃碼支付乘車.該公司某線路公交車隊統計了活動推廣期第一周內使用掃碼支付的情況,其中![]() (單位:天)表示活動推出的天次,
(單位:天)表示活動推出的天次,![]() (單位:十人次)表示當天使用掃碼支付的人次,整理后得到如圖所示的統計表1和散點圖.
(單位:十人次)表示當天使用掃碼支付的人次,整理后得到如圖所示的統計表1和散點圖.
表1:
x | 第1天 | 第2天 | 第3天 | 第4天 | 第5天 | 第6天 | 第7天 |
y | 7 | 12 | 20 | 33 | 54 | 90 | 148 |

(1)由散點圖分析后,可用![]() 作為該線路公交車在活動推廣期使用掃碼支付的人次
作為該線路公交車在活動推廣期使用掃碼支付的人次![]() 關于活動推出天次
關于活動推出天次![]() 的回歸方程,根據表2的數據,求此回歸方程,并預報第8天使用掃碼支付的人次(精確到整數).
的回歸方程,根據表2的數據,求此回歸方程,并預報第8天使用掃碼支付的人次(精確到整數).
表2:
|
|
| img src="http://thumb.zyjl.cn/questionBank/Upload/2019/08/08/08/88254471/SYS201908080801220877999013_ST/SYS201908080801220877999013_ST.008.png" width="67" height="40" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" /> |
|
|
4 | 52 | 3.5 | 140 | 2069 | 112 |
表中![]() ,
,![]() .
.
(2)推廣期結束后,該車隊對此期間乘客的支付情況進行統計,結果如表3.
表3:
支付方式 | 現金 | 乘車卡 | 掃碼 |
頻率 | 10% | 60% | 30% |
優惠方式 | 無優惠 | 按7折支付 | 隨機優惠(見下面統計結果) |
統計結果顯示,掃碼支付中享受5折支付的頻率為![]() ,享受7折支付的頻率為
,享受7折支付的頻率為![]() ,享受9折支付的頻率為
,享受9折支付的頻率為![]() .已知該線路公交車票價為1元,將上述頻率作為相應事件發生的概率,記隨機變量
.已知該線路公交車票價為1元,將上述頻率作為相應事件發生的概率,記隨機變量![]() 為在活動期間該線路公交車搭載乘客一次的收入(單位:元),求
為在活動期間該線路公交車搭載乘客一次的收入(單位:元),求![]() 的分布列和期望.
的分布列和期望.
參考公式:對于一組數據![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估計分別為
的斜率和截距的最小二乘估計分別為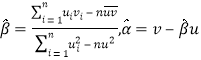 參考數據:
參考數據:![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知定點![]() ,
,![]() ,直線
,直線![]() 、
、![]() 相交于點
相交于點![]() ,且它們的斜率之積為
,且它們的斜率之積為![]() ,記動點
,記動點![]() 的軌跡為曲線
的軌跡為曲線![]() 。
。
(1)求曲線![]() 的方程;
的方程;
(2)過點![]() 的直線與曲線
的直線與曲線![]() 交于
交于![]() 、
、![]() 兩點,是否存在定點
兩點,是否存在定點![]() ,使得直線
,使得直線![]() 與
與![]() 斜率之積為定值,若存在,求出
斜率之積為定值,若存在,求出![]() 坐標;若不存在,請說明理由。
坐標;若不存在,請說明理由。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某種賭博每局的規則是:賭客先在標記有1,2,3,4,5的卡片中隨機摸取一張,將卡片上的數字作為其賭金;隨后放回該卡片,再隨機摸取兩張,將這兩張卡片上數字之差的絕對值的1.4倍作為其獎金.若隨機變量ξ1和ξ2分別表示賭客在一局賭博中的賭金和獎金,則D(ξ1)=_____,E(ξ1)﹣E(ξ2)=_____.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,四棱錐V﹣ABCD中,底面ABCD是菱形,對角線AC與BD交于點O,VO⊥平面ABCD,E是棱VC的中點.
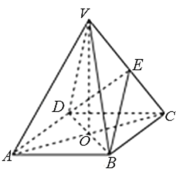
(1)求證:VA∥平面BDE;
(2)求證:平面VAC⊥平面BDE.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某車間4小時內生產了100根不同規格的三角鋼材(單位:厘米),以![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分組的頻率分布直方圖如圖.
分組的頻率分布直方圖如圖.
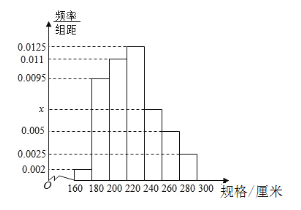
(1)求直方圖中![]() 的值;
的值;
(2)求這批鋼材規格的眾數;
(3)在規格為![]() ,
,![]() ,
,![]() ,
,![]() 的四組鋼材中,用分層抽樣的方法抽取11根鋼材,則在
的四組鋼材中,用分層抽樣的方法抽取11根鋼材,則在![]() 的規格中應抽取多少根?
的規格中應抽取多少根?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com