【題目】對某兩名高三學生連續9次數學測試的成績（單位：分）進行統計得到如下折線圖.下列有關這兩名學生數學成績的分析中，正確的結論是（ ）
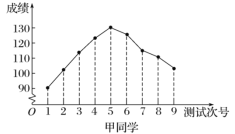
A.甲同學的成績折線圖具有較好的對稱性，與正態曲線相近，故而平均成績為130分
B.根據甲同學成績折線圖中的數據進行統計，估計該同學平均成績在區間
內
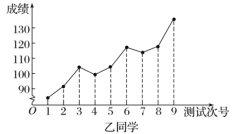
C.乙同學的數學成績與測試次號具有比較明顯的線性相關性，且為正相關
D.乙同學在這連續九次測驗中的最高分與最低分的差超過40分
應用題作業本系列答案科目：高中數學 來源： 題型：
【題目】在直角坐標系
中，橢圓
經過點
，右焦點
到右準線和左頂點的距離相等，經過點的直線
交橢圓于點
.
（1）求橢圓
的標準方程；
（2）點
是直線上在橢圓外的一點，且
，證明：點在定直線上.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】為踐行“綠水青山就是金山銀山”的國家發展戰略，我市對某轄區內畜牧、化工、煤炭三類行業共200個單位的生態環境治理成效進行了考核評估，考評分數達到85分及其以上的單位被稱為“
類”環保單位，未達到85分的單位被稱為“
類”環保單位.現通過分層抽樣的方法確定了這三類行業共20個單位進行調研，統計考評分數如下：
畜牧類行業：85，92，77，81，89，87
化工類行業：79，77，90，85，83，91
煤炭類行業：87，89，76，84，75，94，90，88
（1）計算該轄區這三類行業中每類行業的單位個數；
（2）若從畜牧類行業這六個單位中，再隨機選取兩個單位進行生產效益調查，求選出的這兩個單位中既有“類”環保單位，又有“類”環保單位的概率.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某市移動公司為了提高服務質量，決定對使用A，B兩種套餐的集團用戶進行調查，準備從本市
個人數超過1000人的大集團和8個人數低于200人的小集團中隨機抽取若干個集團進行調查，若一次抽取2個集團，全是小集團的概率為
．
求n的值；
若取出的2個集團是同一類集團，求全為大集團的概率；
若一次抽取4個集團，假設取出小集團的個數為X，求X的分布列和期望．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
，以下結論正確的個數為（ ）
①當
時，函數
的圖象的對稱中心為
；
②當
時，函數在
上為單調遞減函數；
③若函數在上不單調，則
；
④當
時，在
上的最大值為15．
A.1B.2C.3D.4
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知數列
滿足
，其中
是數列
的前
項和．
（1）若數列是首項為
，公比為
的等比數列，求數列
的通項公式；
（2）若
，
，求數列的通項公式；
（3）在（2）的條件下，設
，求證：數列
中的任意一項總可以表示成該數列其他兩項之積．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在學習強國活動中，某市圖書館的科技類圖書和時政類圖書是市民借閱的熱門圖書.為了豐富圖書資源，現對已借閱了科技類圖書的市民（以下簡稱為“問卷市民”）進行隨機問卷調查，若不借閱時政類圖書記1分，若借閱時政類圖書記2分，每位市民選擇是否借閱時政類圖書的概率均為
，市民之間選擇意愿相互獨立.
（1）從問卷市民中隨機抽取4人，記總得分為隨機變量
，求的分布列和數學期望；
（2）（i）若從問卷市民中隨機抽取
人，記總分恰為
分的概率為
，求數列
的前10項和；
（ⅱ）在對所有問卷市民進行隨機問卷調查過程中，記已調查過的累計得分恰為
分的概率為
（比如：
表示累計得分為1分的概率，
表示累計得分為2分的概率，
），試探求與
之間的關系，并求數列
的通項公式.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
