Question

【題目】若函數f（x）=x3﹣ x2+bx+c在x=1時取得極值，且當x∈[﹣1，2]時，f（x）＜c2恒成立．
（1）求實數b的值；
（2）求實數c的取值范圍．

Answer 1

【答案】
（1）解：∵f（x）=x3﹣ x2+bx+c，

∴f′（x）=3x2﹣x+b，

∵x=1是方程3x2﹣x+b=0的一個根，

設另一個根是x0，則 ，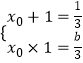

∴x0=﹣ ，b=﹣2

（2）解：由（1）知，f（x）=x3﹣ x2﹣2x+c，

∴f′（x）=3x2﹣x﹣2=（3x+2）（x﹣1），

令f′（x）=0，解得x1=﹣ ，x2=1；

列表如下：

x	[﹣1，﹣ ）	﹣	（﹣ ，1）	1	（1，2]
f′（x）	+	0	﹣	0	+
f（x）	單調遞增	極大值 +c	單調遞減	極小值	單調遞增

由表格知，f（x）取得極大值f（﹣ ）= +c，

又f（2）=2+c，

∴當x=2時，函數取得最大值f（x）max=2+c；

∴2+c＜c2，

解得c＜﹣1或c＞2，

∴c的取值范圍是（﹣∞，﹣1）∪（2，+∞）

【解析】（1）求出f（x）的導數f′（x），由函數的零點以及根與系數的關系求出b的值；（2）利用導數求出f（x）在閉區間[﹣1，2]上的最大值f（x）max ， 令其小于c2 ， 求出c的取值范圍．
【考點精析】利用函數的極值與導數和函數的最大(小)值與導數對題目進行判斷即可得到答案，需要熟知求函數的極值的方法是:（1）如果在附近的左側,右側,那么是極大值（2）如果在附近的左側,右側,那么是極小值；求函數在上的最大值與最小值的步驟：（1）求函數在內的極值；（2）將函數的各極值與端點處的函數值，比較，其中最大的是一個最大值，最小的是最小值．