
【題目】已知函數f(x)= ![]() 為偶函數
為偶函數
(1)求實數a的值;
系;
(2)記集合E={y|y=f(x),x∈{﹣1,1,2}},λ=lg22+lg2lg5+lg5﹣ ![]() ,判斷λ與E的
,判斷λ與E的
(3)當x∈[ ![]() ,
, ![]() ](m>0,n>0)時,若函數f(x)的值域[2﹣3m,2﹣3n],求實數m,n值.
](m>0,n>0)時,若函數f(x)的值域[2﹣3m,2﹣3n],求實數m,n值.
【答案】
(1)解:∵函數 ![]() 為偶函數.
為偶函數.
∴f(﹣x)=f(x)
即 ![]() =
= ![]()
∴2(a+1)x=0,
∵x為非零實數,
∴a+1=0,即a=﹣1
(2)解:由(1)得 ![]()
∴E={y|y=f(x),x∈{﹣1,1,2}}={0, ![]() }
}
而 ![]() =
= ![]() =
= ![]() =
= ![]() =
= ![]()
∴λ∈E
(3)解:∵ ![]() >0恒成立
>0恒成立
∴ ![]() 在
在 ![]() 上為增函數
上為增函數
又∵函數f(x)的值域為[2﹣3m,2﹣3n],
∴f( ![]() )=1﹣m2=2﹣3m,且f(
)=1﹣m2=2﹣3m,且f( ![]() )=1﹣n2=2﹣3n,
)=1﹣n2=2﹣3n,
又∵ ![]() ,m>0,n>0
,m>0,n>0
∴m>n>0
解得m= ![]() ,n=
,n= ![]()
【解析】(1)根據函數 ![]() 為偶函數f(﹣x)=f(x),構造關于a的方程組,可得a值;(2)由(1)中函數f(x)的解析式,將x∈{﹣1,1,2}代入求出集合E,利用對數的運算性質求出λ,進而根據元素與集合的關系可得答案(3)求出函數f(x)的導函數,判斷函數的單調性,進而根據函數f(x)的值域為[2﹣3m,2﹣3n],x∈
為偶函數f(﹣x)=f(x),構造關于a的方程組,可得a值;(2)由(1)中函數f(x)的解析式,將x∈{﹣1,1,2}代入求出集合E,利用對數的運算性質求出λ,進而根據元素與集合的關系可得答案(3)求出函數f(x)的導函數,判斷函數的單調性,進而根據函數f(x)的值域為[2﹣3m,2﹣3n],x∈ ![]() ,m>0,n>0構造關于m,n的方程組,進而得到m,n的值.
,m>0,n>0構造關于m,n的方程組,進而得到m,n的值.
【考點精析】解答此題的關鍵在于理解奇偶性與單調性的綜合的相關知識,掌握奇函數在關于原點對稱的區間上有相同的單調性;偶函數在關于原點對稱的區間上有相反的單調性,以及對利用導數研究函數的單調性的理解,了解一般的,函數的單調性與其導數的正負有如下關系: 在某個區間![]() 內,(1)如果
內,(1)如果![]() ,那么函數
,那么函數![]() 在這個區間單調遞增;(2)如果
在這個區間單調遞增;(2)如果![]() ,那么函數
,那么函數![]() 在這個區間單調遞減.
在這個區間單調遞減.


 孟建平小學滾動測試系列答案
孟建平小學滾動測試系列答案 黃岡天天練口算題卡系列答案
黃岡天天練口算題卡系列答案科目:高中數學 來源: 題型:
【題目】設l,m是兩條不同的直線,α是一個平面,則下列命題正確的是( )
A.若l⊥m,mα,則l⊥α
B.若l⊥α,l∥m,則m⊥α
C.若l∥α,mα,則l∥m
D.若l∥α,m∥α,則l∥m
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校100名學生期中考試數學成績的頻率分布直方圖如圖,其中成績分組區間如下:
組號 | 第一組 | 第二組 | 第三組 | 第四組 | 第五組 |
分組 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
(Ⅰ)求圖中a的值;
(Ⅱ)根據頻率分布直方圖,估計這100名學生期中考試數學成績的平均分;
(Ⅲ)現用分層抽樣的方法從第3、4、5組中隨機抽取6名學生,將該樣本看成一個總體,從中隨機抽取2名,求其中恰有1人的分數不低于90分的概率?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知中心在原點,焦點在![]() 軸上的橢圓的一個焦點為
軸上的橢圓的一個焦點為![]() ,
, 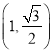 是橢圓上的一個點.
是橢圓上的一個點.
(1)求橢圓的標準方程;
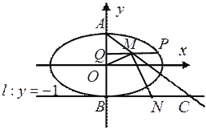
(2)設橢圓的上、下頂點分別為![]() ,
, ![]() (
(![]() )是橢圓上異于
)是橢圓上異于![]() 的任意一點,
的任意一點, ![]() 軸,
軸, ![]() 為垂足,
為垂足, ![]() 為線段
為線段![]() 中點,直線
中點,直線![]() 交直線
交直線![]() 于點
于點![]() ,
, ![]() 為線段
為線段![]() 的中點,如果
的中點,如果![]() 的面積為
的面積為![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】定義在R上的偶函數f(x)滿足f(x+1)= ![]() ,且f(x)在[﹣3,﹣2]上是減函數,若α,β是銳角三角形的兩個內角,則( )
,且f(x)在[﹣3,﹣2]上是減函數,若α,β是銳角三角形的兩個內角,則( )
A.f(sinα)>f(sinβ)
B.f(cosα)>f(cosβ)
C.f(sinα)>f(cosβ)
D.f(sinα)<f(cosβ)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=mx2﹣mx﹣1.
(1)若對于x∈R,f(x)<0恒成立,求實數m的取值范圍;
(2)若對于x∈[1,3],f(x)<5﹣m恒成立,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】將直線2x﹣y+λ=0沿x軸向左平移1個單位,所得直線與圓x2+y2+2x﹣4y=0相切,則實數λ的值為( )
A.﹣3或7
B.﹣2或8
C.0或10
D.1或11
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an}的前n項和Sn= ![]() ,n∈N* .
,n∈N* .
(Ⅰ)求數列{an}的通項公式;
(Ⅱ)設bn= ![]() +(﹣1)nan , 求數列{bn}的前2n項和.
+(﹣1)nan , 求數列{bn}的前2n項和.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com