
���}Ŀ����֪![]() ������(g��)��c(di��n)��
������(g��)��c(di��n)��![]() ��
�� ![]() ��
��![]() �����c(di��n).��
�����c(di��n).��
(1) ![]() ����ֱ���ķ��̣�
����ֱ���ķ��̣�
(2) ![]() ߅���о�
߅���о�![]() ����ֱ���ķ��̣�
����ֱ���ķ��̣�
(3) ![]() ߅�ϵĴ�ֱƽ�־�
߅�ϵĴ�ֱƽ�־�![]() �ķ��̣�
�ķ��̣�
���𰸡���1��x+2y-4=0����2��2x-3y+6=0����3��y=2x+2��
��������ԇ�}��������1��ֱ�����̵ă��c(di��n)ʽ���![]() ����ֱ���ķ��̣���2������BC�����c(di��n)D����(bi��o)�飨0,2������ֱ�����̵Ľؾ�ʽ���AD����ֱ�����̣���3�����ֱ��)BC��б��
����ֱ���ķ��̣���2������BC�����c(di��n)D����(bi��o)�飨0,2������ֱ�����̵Ľؾ�ʽ���AD����ֱ�����̣���3�����ֱ��)BC��б��![]() ���Ƀ�ֱ����ֱ�ėl�����ֱ��DE��б��
���Ƀ�ֱ����ֱ�ėl�����ֱ��DE��б��![]() �����ɽؾ�ʽ���DE�ķ��̡�
�����ɽؾ�ʽ���DE�ķ��̡�
ԇ�}������(1)��?y��n)�ֱ��BC��(j��ng)�^B(2��1)��C(-2��3)���c(di��n)��
�Ƀ��c(di��n)ʽ��BC�ķ��̞�y-1= (x-2)��
��x+2y-4=0��
(2)�O(sh��)BC���c(di��n)D������(bi��o)��(x��y)���tx=0��y=2��
BC߅���о�AD�^�c(di��n)A(-3��0)��D(0��2)���c(di��n)���ɽؾ�ʽ��
AD����ֱ�����̞�=1����2x-3y+6=0��
(3)BC��б��![]() ���tBC�Ĵ�ֱƽ�־�DE��б��k2=2��
���tBC�Ĵ�ֱƽ�־�DE��б��k2=2��
��б��ʽ��ֱ��DE�ķ��̞�y=2x+2��


 ȫ�ܾ�����ϵ�д�
ȫ�ܾ�����ϵ�д�
| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)f��x��=��x��a����x��b��������a��b������f��x���ĈD����D��ʾ���t����(sh��)g��x��=ax+b�ĈD����飨������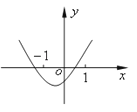
A.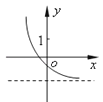
B.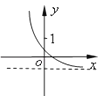
C.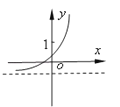
D.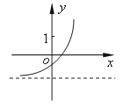
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ���x��4-4������(bi��o)ϵ�c����(sh��)����
��ֱ֪��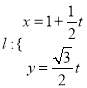 ��
��![]() �酢��(sh��)��������
�酢��(sh��)��������![]() ��
��![]() �酢��(sh��)����
�酢��(sh��)����
��1���O(sh��)![]() �c
�c![]() �ཻ��
�ཻ��![]() ���c(di��n)����
���c(di��n)����![]() ��
��
��2����������![]() �ϸ��c(di��n)�ęM����(bi��o)���s��ԭ����
�ϸ��c(di��n)�ęM����(bi��o)���s��ԭ����![]() �����v����(bi��o)���s��ԭ����
�����v����(bi��o)���s��ԭ����![]() �����õ�����
�����õ�����![]() ���O(sh��)�c(di��n)
���O(sh��)�c(di��n)![]() ������
������![]() �ϵ�һ��(g��)��(d��ng)�c(di��n)��������ֱ��
�ϵ�һ��(g��)��(d��ng)�c(di��n)��������ֱ��![]() �ľ��x����Сֵ��
�ľ��x����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ��ijУ�ĸ߶��꼉(j��)�W(xu��)�����S�C(j��)��ȡ60���W(xu��)�����������п�ԇ�����γɿ�����������(sh��)���ֳ����Σ� ![]() ��
�� ![]() ��
�� ![]() ����
����![]() ��õ������l�ʷֲ�ֱ���D.
��õ������l�ʷֲ�ֱ���D.
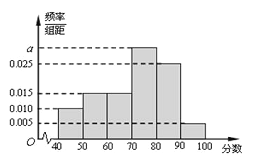
(1)����(j��)�l�ʷֲ�ֱ���D����Ӌ(j��)ԓУ�߶��꼉(j��)�W(xu��)�����п�ԇ���γɿ�����λ��(sh��)�����_��0.1��������(sh��)��ƽ����(sh��)��
(2)�÷ӳ�ӵķ�����ȡһ��(g��)������20�Ęӱ��������?j��n)?sh��)�γ�ȡ���˔�(sh��).
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����D���E�A![]() �c�p����
�c�p����![]() ����ͬ�Ľ��c(di��n)
����ͬ�Ľ��c(di��n)![]() ��
��![]() ������?c��)?/span>
������?c��)?/span>![]() �S�҂�(c��)�Ѓɂ�(g��)���c(di��n)
�S�҂�(c��)�Ѓɂ�(g��)���c(di��n)![]() ��
��![]() ���M��
���M��![]() .��ֱ��
.��ֱ��![]() ���(c��)�ęE�A���֣���
���(c��)�ęE�A���֣���![]() ��
�� ![]() ���c(di��n)��ӛ������
���c(di��n)��ӛ������![]() ��ֱ��
��ֱ��![]() �҂�(c��)���p�������֣�����
�҂�(c��)���p�������֣�����![]() ��
�� ![]() ���c(di��n)��ӛ������
���c(di��n)��ӛ������![]() .��
.��![]() ����c(di��n)��һ�l�侀���քe��
����c(di��n)��һ�l�侀���քe��![]() ���c(di��n)
���c(di��n)![]() ����
����![]() ���c(di��n)
���c(di��n)![]() ���c(di��n)
���c(di��n)![]() �ڵ�һ���ޣ����O(sh��)�˕r(sh��)
�ڵ�һ���ޣ����O(sh��)�˕r(sh��)![]() .
.
��1����![]() �ķ��̣�
�ķ��̣�
��2���C���� ![]() ����̽��ֱ��
����̽��ֱ��![]() �c
�c![]() б��֮�g���P(gu��n)ϵ��
б��֮�g���P(gu��n)ϵ��
��3���O(sh��)ֱ��![]() ��
��![]() ���c(di��n)
���c(di��n)![]() ����
����![]() ����e
����e![]() ��ȡֵ����.
��ȡֵ����.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����D���ڎ��wABDCE�У�AB=AD��AE��ƽ��ABD��M�龀��BD�����c(di��n)��MC��AE��AE=MC��
��1�����C��ƽ��BCD��ƽ��CDE��
��2����N�龀��DE�����c(di��n)�����C��ƽ��AMN��ƽ��BEC��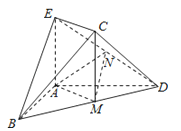
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����D��AB��A�����S��CD�����ֱ����E�����A����һ�c(di��n)��AB=1��CD=2��CE=DE��
��1�������FA��CDE��ȫ��e��
��2���c(di��n)D��ƽ��ACE�ľ��x��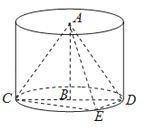
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
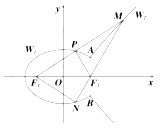
���}Ŀ����֪![]() ����c(di��n)
����c(di��n)![]() ��
�� ![]() ߅�ϵ��о�
߅�ϵ��о�![]() ����ֱ�����̞�
����ֱ�����̞�![]() ��
�� ![]() ߅�ϵĸ�
߅�ϵĸ�![]() ����ֱ�����̞�
����ֱ�����̞�![]() ����
����
��1�����c(di��n)![]() ������(bi��o)��
������(bi��o)��
��2����ֱ��![]() �ķ��̣�
�ķ��̣�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪�^���タ![]() ���c(di��n)
���c(di��n)![]() �҃Aб�ǵ�
�҃Aб�ǵ�![]() ֱ��
ֱ��![]() �c���タ
�c���タ![]() �����c(di��n)
�����c(di��n)![]()
![]() ����e��
����e��![]() ��
��
��I�����タ![]() �ķ��̣�
�ķ��̣�
��II���O(sh��)![]() ��ֱ��
��ֱ��![]() �ϵ�һ��(g��)��(d��ng)�c(di��n)���^
�ϵ�һ��(g��)��(d��ng)�c(di��n)���^![]() �����タ
�����タ![]() ���о������c(di��n)�քe��
���о������c(di��n)�քe��![]() ֱ��
ֱ��![]() �cֱ��
�cֱ��![]() �S�Ľ��c(di��n)�քe��
�S�Ľ��c(di��n)�քe��![]() �c(di��n)
�c(di��n)![]() ����
����![]() ��A��
��A��![]() ��돽�ĈA��������c(di��n)����
��돽�ĈA��������c(di��n)����![]() ���r(sh��)�c(di��n)
���r(sh��)�c(di��n)![]() ������(bi��o)��
������(bi��o)��
�鿴�𰸺ͽ���>>
���H�W(xu��)У��(y��u)�x - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com