【題目】設二階矩陣A＝
.
（1） 求A－1；
（2） 若曲線C在矩陣A對應的變換作用下得到曲線C′：6x2－y2＝1，求曲線C的方程．
一課一練課時達標系列答案科目：高中數學 來源： 題型：
【題目】某少兒游泳隊需對隊員進行限時的仰臥起坐達標測試.已知隊員的測試分數
與仰臥起坐
個數
之間的關系如下：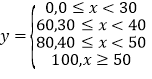
；測試規則：每位隊員最多進行三組測試，每組限時1分鐘，當一組測完，測試成績達到60分或以上時，就以此組測試成績作為該隊員的成績，無需再進行后續的測試，最多進行三組；根據以往的訓練統計，隊員“喵兒”在一分鐘內限時測試的頻率分布直方圖如下：
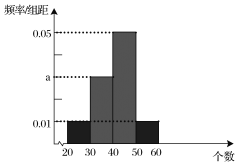
（1）計算
值；
（2）以此樣本的頻率作為概率，求
①在本次達標測試中，“喵兒”得分等于
的概率；
②“喵兒”在本次達標測試中可能得分的分布列及數學期望.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
的左頂點為A1，右焦點為F2，過點F2作垂直于x軸的直線交該橢圓于M、N兩點，直線A1M的斜率為
．
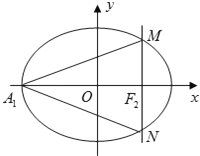
（Ⅰ）求橢圓的離心率；
（Ⅱ）若△A1MN的外接圓在M處的切線與橢圓相交所得弦長為
，求橢圓方程．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知動圓M與直線
相切，且與圓N：
外切
（1）求動圓圓心M的軌跡C的方程；
（2）點O為坐標原點，過曲線C外且不在y軸上的點P作曲線C的兩條切線，切點分別記為A，B，當直線
與
的斜率之積為
時，求證：直線過定點.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某港口某天0時至24時的水深
（米）隨時間
（時）變化曲線近似滿足如下函數模型
（
）.若該港口在該天0時至24時內，有且只有3個時刻水深為3米，則該港口該天水最深的時刻不可能為（ ）
A.16時B.17時C.18時D.19時
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】以下說法：
①將一組數據中的每一個數據都加上或減去同一個常數后，方差不變；
②設有一個回歸方程
，變量
增加1個單位時，
平均增加5個單位
③線性回歸方程
必過
④設具有相關關系的兩個變量
的相關系數為
，那么
越接近于0，之間的線性相關程度越高；
⑤在一個
列聯表中，由計算得
的值，那么的值越大，判斷兩個變量間有關聯的把握就越大。
其中錯誤的個數是（ ）
A.0B.1C.2D.3
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】“不忘初心、牢記使命”主題教育活動正在全國開展，某區政府為統計全區黨員干部一周參與主題教育活動的時間，從全區的黨員干部中隨機抽取n名，獲得了他們一周參加主題教育活動的時間（單位：時）的頻率分布直方圖，如圖所示，已知參加主題教育活動的時間在
內的人數為92.
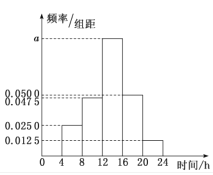
（1）估計這些黨員干部一周參與主題教育活動的時間的平均值；
（2）用頻率估計概率，如果計劃對全區一周參與主題教育活動的時間在
內的黨員干部給予獎勵，且參與時間在
，
內的分別獲二等獎和一等獎，通過分層抽樣方法從這些獲獎人中隨機抽取5人，再從這5人中任意選取3人，求3人均獲二等獎的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
