
【題目】設(shè)函數(shù)![]() ,
,![]() .
.
(1)求函數(shù)![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(2)當(dāng)![]() 時,討論函數(shù)
時,討論函數(shù)![]() 與
與![]() 圖象的交點個數(shù).
圖象的交點個數(shù).
【答案】(1)當(dāng)![]() 時,函數(shù)
時,函數(shù)![]() 的單調(diào)增區(qū)間是
的單調(diào)增區(qū)間是![]() ,無單調(diào)減區(qū)間;當(dāng)
,無單調(diào)減區(qū)間;當(dāng)![]() 時,函數(shù)
時,函數(shù)![]() 的單調(diào)增區(qū)間是
的單調(diào)增區(qū)間是![]() ,單調(diào)減區(qū)間是
,單調(diào)減區(qū)間是![]() ;(2)1個.
;(2)1個.
【解析】
(1)先求出函數(shù)的導(dǎo)數(shù),解關(guān)于導(dǎo)函數(shù)的不等式,從而求出函數(shù)的單調(diào)區(qū)間;
(2)問題轉(zhuǎn)化為求函數(shù)![]() 的零點個數(shù)問題,通過求導(dǎo),得到函數(shù)
的零點個數(shù)問題,通過求導(dǎo),得到函數(shù)![]() 的單調(diào)區(qū)間,求出
的單調(diào)區(qū)間,求出![]() 的極小值,從而求出函數(shù)
的極小值,從而求出函數(shù)![]() 的零點個數(shù)即
的零點個數(shù)即![]() 和
和![]() 的交點個數(shù).
的交點個數(shù).
(1)函數(shù)![]() 的定義域為
的定義域為![]() ,
,![]() ,
,
當(dāng)![]() 時,
時,![]() ,所以函數(shù)
,所以函數(shù)![]() 的單調(diào)增區(qū)間是
的單調(diào)增區(qū)間是![]() ,無單調(diào)減區(qū)間;
,無單調(diào)減區(qū)間;
當(dāng)![]() 時,
時,![]() ;
;
當(dāng)![]() 時,
時,![]() ,函數(shù)
,函數(shù)![]() 單調(diào)遞減;當(dāng)
單調(diào)遞減;當(dāng)![]() 時,
時,![]() ,函數(shù)
,函數(shù)![]() 單調(diào)遞增.
單調(diào)遞增.
綜上,當(dāng)![]() 時,函數(shù)
時,函數(shù)![]() 的單調(diào)增區(qū)間是
的單調(diào)增區(qū)間是![]() ,無單調(diào)減區(qū)間;
,無單調(diào)減區(qū)間;
當(dāng)![]() 時,函數(shù)
時,函數(shù)![]() 的單調(diào)增區(qū)間是
的單調(diào)增區(qū)間是![]() ,單調(diào)減區(qū)間是
,單調(diào)減區(qū)間是![]() .
.
(2)令![]()
![]() ,
,![]() ,問題等價于求函數(shù)
,問題等價于求函數(shù)![]() 的零點個數(shù),
的零點個數(shù),
當(dāng)![]() 時,
時,![]() ,
,![]() ,有唯一零點;
,有唯一零點;
當(dāng)![]() 時,
時,![]() ,
,
當(dāng)![]() 時,
時,![]() ,函數(shù)
,函數(shù)![]() 為減函數(shù),注意到
為減函數(shù),注意到![]() ,
,![]() ,所以
,所以![]() 有唯一零點;
有唯一零點;
當(dāng)![]() 時,由
時,由![]() 得
得![]() 或
或![]() ,由
,由![]() 得
得![]() ,所以函數(shù)
,所以函數(shù)![]() 在
在![]() 和
和![]() 上單調(diào)遞減,在
上單調(diào)遞減,在![]() 上單調(diào)遞增,注意到
上單調(diào)遞增,注意到![]() ,
,
![]() ,
,
所以![]() 有唯一零點;
有唯一零點;
當(dāng)![]() 時,由
時,由![]() 得,
得,![]() 或
或![]() ,
,
由![]() 得
得![]() ,
,
所以函數(shù)![]() 在
在![]() 和
和![]() 單調(diào)遞減,在
單調(diào)遞減,在![]() 單調(diào)遞增,又
單調(diào)遞增,又![]() ,
,
所以![]() ,
,
而![]() ,所以
,所以![]() 有唯一零點.
有唯一零點.
綜上,函數(shù)![]() 有唯一零點,即當(dāng)
有唯一零點,即當(dāng)![]() 時函數(shù)
時函數(shù)![]() 與
與![]() 圖象總有一個交點.
圖象總有一個交點.


科目:高中數(shù)學(xué) 來源: 題型:
【題目】2019年1月3日嫦娥四號探測器成功實現(xiàn)人類歷史上首次月球背面軟著陸,我國航天事業(yè)取得又一重大成就,實現(xiàn)月球背面軟著陸需要解決的一個關(guān)鍵技術(shù)問題是地面與探測器的通訊聯(lián)系.為解決這個問題,發(fā)射了嫦娥四號中繼星“鵲橋”,鵲橋沿著圍繞地月拉格朗日![]() 點的軌道運行.
點的軌道運行.![]() 點是平衡點,位于地月連線的延長線上.設(shè)地球質(zhì)量為M1,月球質(zhì)量為M2,地月距離為R,
點是平衡點,位于地月連線的延長線上.設(shè)地球質(zhì)量為M1,月球質(zhì)量為M2,地月距離為R,![]() 點到月球的距離為r,根據(jù)牛頓運動定律和萬有引力定律,r滿足方程:
點到月球的距離為r,根據(jù)牛頓運動定律和萬有引力定律,r滿足方程:
![]() .
.
設(shè)![]() ,由于
,由于![]() 的值很小,因此在近似計算中
的值很小,因此在近似計算中![]() ,則r的近似值為
,則r的近似值為
A.  B.
B. 
C.  D.
D. 
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】
已知曲線![]() 上的點到點
上的點到點![]() 的距離比它到直線
的距離比它到直線![]() 的距離小2.
的距離小2.
(1)求曲線![]() 的方程;
的方程;
(2)曲線![]() 在點
在點![]() 處的切線
處的切線![]() 與
與![]() 軸交于點
軸交于點![]() .直線
.直線![]() 分別與直線
分別與直線![]() 及
及![]() 軸交于點
軸交于點![]() ,以
,以![]() 為直徑作圓
為直徑作圓![]() ,過點
,過點![]() 作圓
作圓![]() 的切線,切點為
的切線,切點為![]() ,試探究:當(dāng)點
,試探究:當(dāng)點![]() 在曲線
在曲線![]() 上運動(點
上運動(點![]() 與原點不重合)時,線段
與原點不重合)時,線段![]() 的長度是否發(fā)生變化?證明你的結(jié)論.
的長度是否發(fā)生變化?證明你的結(jié)論.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖所示,某鎮(zhèn)有一塊空地![]() ,其中
,其中![]() ,
,![]() ,
,![]() .當(dāng)?shù)劓?zhèn)政府規(guī)劃將這塊空地改造成一個旅游景點,擬在中間挖一個人工湖
.當(dāng)?shù)劓?zhèn)政府規(guī)劃將這塊空地改造成一個旅游景點,擬在中間挖一個人工湖![]() ,其中
,其中![]() ,
,![]() 都在邊
都在邊![]() 上,且
上,且![]() ,挖出的泥土堆放在
,挖出的泥土堆放在![]() 地帶上形成假山,剩下的
地帶上形成假山,剩下的![]() 地帶開設(shè)兒童游樂場.為安全起見,需在
地帶開設(shè)兒童游樂場.為安全起見,需在![]() 的周圍安裝防護網(wǎng).
的周圍安裝防護網(wǎng).

(1)當(dāng)![]() 時,求防護網(wǎng)的總長度;
時,求防護網(wǎng)的總長度;
(2)為節(jié)省投入資金,人工湖![]() 的面積要盡可能小,問如何設(shè)計施工方案,可使
的面積要盡可能小,問如何設(shè)計施工方案,可使![]() 的面積最小?最小面積是多少?
的面積最小?最小面積是多少?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 是直角梯形,側(cè)棱
是直角梯形,側(cè)棱![]() 底面
底面![]() ,
,![]() 垂直于
垂直于![]() 和
和![]() ,
,![]() 為棱
為棱![]() 上的點,
上的點,![]() ,
,![]() .
.
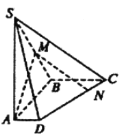
(1)若![]() 為棱
為棱![]() 的中點,求證:
的中點,求證:![]() 平面
平面![]() ;
;
(2)當(dāng)![]() 時,求平面
時,求平面![]() 與平面
與平面![]() 所成的銳二面角的余弦值;
所成的銳二面角的余弦值;
(3)在第(2)問條件下,設(shè)點![]() 是線段
是線段![]() 上的動點,
上的動點,![]() 與平面
與平面![]() 所成的角為
所成的角為![]() ,求當(dāng)
,求當(dāng)![]() 取最大值時點
取最大值時點![]() 的位置.
的位置.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖(1),等腰梯形![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 、
、![]() 分別是
分別是![]() 的兩個三等分點.若把等腰梯形沿虛線
的兩個三等分點.若把等腰梯形沿虛線![]() 、
、![]() 折起,使得點
折起,使得點![]() 和點
和點![]() 重合,記為點
重合,記為點![]() ,如圖(2).
,如圖(2).
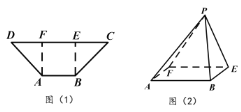
(Ⅰ)求證:平面![]() 平面
平面![]() ;
;
(Ⅱ)求平面![]() 與平面
與平面![]() 所成銳二面角的余弦值.
所成銳二面角的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() :
:![]() 的左
的左![]() 、
、![]() 右焦點分別為,點
右焦點分別為,點![]() 在橢圓上,且滿足
在橢圓上,且滿足![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)設(shè)傾斜角為![]() 的直線
的直線![]() 與
與![]() 交于
交于![]() ,
,![]() 兩點,記
兩點,記![]() 的面積為
的面積為![]() ,求
,求![]() 取最大值時直線
取最大值時直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】現(xiàn)采用隨機模擬的方法估計某運動員射擊4次,至少擊中3次的概率;先由計算器給出0到9之間取整數(shù)值的隨機數(shù),指定0、1、2表示沒有擊中目標(biāo),3、4、5、6、7、8、9表示擊中目標(biāo),以4個隨機數(shù)為一組,代表射擊4次的結(jié)果,經(jīng)隨機模擬產(chǎn)生了20隨機數(shù):![]()
![]()
根據(jù)以上數(shù)據(jù)估計該射擊運動員射擊4次至少擊中3次的概率為( )
A.0.55B.0.6C.0.65D.0.7
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com