
【題目】已知直線![]() 的方程為
的方程為![]() ,若
,若![]() 在
在![]() 軸上的截距為
軸上的截距為![]() ,且
,且![]() .
.
(1)求直線![]() 和
和![]() 的交點坐標(biāo);
的交點坐標(biāo);
(2)已知直線![]() 經(jīng)過
經(jīng)過![]() 與
與![]() 的交點,且在
的交點,且在![]() 軸上截距是在
軸上截距是在![]() 軸上的截距的2倍,求
軸上的截距的2倍,求![]() 的方程.
的方程.
【答案】(1)交點為![]() ;(2)
;(2)![]() 的方程為
的方程為![]() 或
或![]()
【解析】
(1)根據(jù)兩直線垂直的關(guān)系,以及直線![]() 在
在![]() 軸上的截距,可得
軸上的截距,可得![]() 方程,聯(lián)立方程,可得結(jié)果.
方程,聯(lián)立方程,可得結(jié)果.
(2)利用(1)的結(jié)論,采用分類討論的方法,可假設(shè)直線![]() 的截距式,利用(1)的結(jié)論,可得結(jié)果.
的截距式,利用(1)的結(jié)論,可得結(jié)果.
(1)由直線![]() 的方程為
的方程為![]() 且
且![]()
可得直線![]() 的斜率為:2,
的斜率為:2,
又![]() 在
在![]() 軸上的截距為
軸上的截距為![]() ,即過點
,即過點![]()
所以直線![]() 方程:
方程:![]()
即![]() ,
,
聯(lián)立![]() 方程,得:
方程,得:
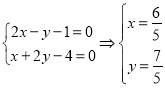 ,
,
故交點為![]()
(2)依據(jù)題意可知:
直線![]() 在
在![]() 軸上截距是在
軸上截距是在![]() 軸上的截距的2倍,
軸上的截距的2倍,
且直線![]() 經(jīng)過
經(jīng)過![]() 與
與![]() 的交點
的交點![]()
當(dāng)直線![]() 原點時,
原點時,![]() 方程為:
方程為:![]()
當(dāng)直線![]() 不過原點時,設(shè)
不過原點時,設(shè)![]() 方程為
方程為![]()
則![]() ,故
,故![]() 方程為:
方程為:![]() ,
,
即![]()
綜上所述:
![]() 的方程為
的方程為![]() 或
或![]()



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知不交于同一點的三條直線![]() :4x+y-4=0,
:4x+y-4=0,![]() :mx+y=0,
:mx+y=0,![]() :x-my-4=0.
:x-my-4=0.
(1)當(dāng)這三條直線不能圍成三角形時,求實數(shù)m的值;
(2)當(dāng)![]() 與
與![]() ,
,![]() 都垂直時,求兩垂足間的距離.
都垂直時,求兩垂足間的距離.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】“總把新桃換舊符”(王安石)、“燈前小草寫桃符”(陸游),春節(jié)是中華民族的傳統(tǒng)節(jié)日,在宋代人們用寫“桃符”的方式來祈福避禍,而現(xiàn)代人們通過貼“福”字、貼春聯(lián)、掛燈籠等方式來表達(dá)對新年的美好祝愿,某商家在春節(jié)前開展商品促銷活動,顧客凡購物金額滿50元,則可以從“福”字、春聯(lián)和燈籠這三類禮品中任意免費(fèi)領(lǐng)取一件,若有4名顧客都領(lǐng)取一件禮品,則他們中有且僅有2人領(lǐng)取的禮品種類相同的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某糕點房推出一類新品蛋糕,該蛋糕的成本價為4元,售價為8元.受保質(zhì)期的影響,當(dāng)天沒有銷售完的部分只能銷毀.經(jīng)過長期的調(diào)研,統(tǒng)計了一下該新品的日需求量.現(xiàn)將近期一個月(30天)的需求量展示如下:
日需求量x(個) | 20 | 30 | 40 | 50 |
天數(shù) | 5 | 10 | 10 | 5 |
(1)從這30天中任取兩天,求兩天的日需求量均為40個的概率.
(2)以上表中的頻率作為概率,列出日需求量![]() 的分布列,并求該月的日需求量
的分布列,并求該月的日需求量![]() 的期望.
的期望.
(3)根據(jù)(2)中的分布列求得當(dāng)該糕點房一天制作35個該類蛋糕時,對應(yīng)的利潤的期望值為![]() ;現(xiàn)有員工建議擴(kuò)大生產(chǎn)一天45個,求利用利潤的期望值判斷此建議該不該被采納.
;現(xiàn)有員工建議擴(kuò)大生產(chǎn)一天45個,求利用利潤的期望值判斷此建議該不該被采納.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)f(x)=log4(4x+1)+kx(k∈R)是偶函數(shù).
(1)求k的值;
(2)設(shè)g(x)=log4![]() ,若函數(shù)f(x)與g(x)的圖象有且只有一個公共點,求實數(shù)a的取值范圍.
,若函數(shù)f(x)與g(x)的圖象有且只有一個公共點,求實數(shù)a的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)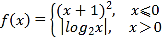 ,若方程f(x)=a有四個不同的解x1,x2,x3,x4,且x1<x2<x3<x4,則
,若方程f(x)=a有四個不同的解x1,x2,x3,x4,且x1<x2<x3<x4,則![]() 的取值范圍為( )
的取值范圍為( )
A. (﹣1,+∞)B. (﹣1,1]C. (﹣∞,1)D. [﹣1,1)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知命題:
p:![]() 是“直線
是“直線![]() 不過第四象限”的充分不必要條件;
不過第四象限”的充分不必要條件;
q:復(fù)數(shù)![]() 在復(fù)平面內(nèi)所對應(yīng)的點在第二象限;
在復(fù)平面內(nèi)所對應(yīng)的點在第二象限;
r:直線![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,則直線
,則直線![]() ∥平面
∥平面![]() ;
;
s:若![]() ,
,![]() 的值越大其圖象越高瘦.
的值越大其圖象越高瘦.
則四個命題中真命題的個數(shù)是
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知命題![]() “存在
“存在![]() ”,命題
”,命題![]() :“曲線
:“曲線![]() 表示焦點在
表示焦點在![]() 軸上的橢圓”,命題
軸上的橢圓”,命題![]() “曲線
“曲線![]() 表示雙曲線”
表示雙曲線”
(1)若“![]() 且
且![]() ”是真命題,求實數(shù)
”是真命題,求實數(shù)![]() 的取值范圍;
的取值范圍;
(2)若![]() 是
是![]() 的必要不充分條件,求實數(shù)
的必要不充分條件,求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() ,
,![]() .
.
(1)求曲線![]() 在點
在點![]() 處的切線方程;
處的切線方程;
(2)證明:當(dāng)![]() 時,曲線
時,曲線![]() 恒在曲線
恒在曲線![]() 的下方;
的下方;
(3)當(dāng)![]() 時,不等式
時,不等式![]() 恒成立,求實數(shù)
恒成立,求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com