
【題目】已知橢圓![]() .點E為橢圓在第一象限內(nèi)一點,點F在橢圓上且與點E關(guān)于原點對稱,直線
.點E為橢圓在第一象限內(nèi)一點,點F在橢圓上且與點E關(guān)于原點對稱,直線![]() 與橢圓交于A,B兩點,則點E,F到直線x+y-1=0的距離之和的最大值是________;此時四邊形AEBF的面積是________.
與橢圓交于A,B兩點,則點E,F到直線x+y-1=0的距離之和的最大值是________;此時四邊形AEBF的面積是________.
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)若![]() 在
在![]() 上存在單調(diào)遞增區(qū)間,求實數(shù)
上存在單調(diào)遞增區(qū)間,求實數(shù)![]() 的取值范圍;
的取值范圍;
(2)設![]() ,若
,若![]() ,恒有
,恒有![]() 成立,求
成立,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】設拋物線![]() 的焦點為
的焦點為![]() ,準線為
,準線為![]() ,
,![]() 為過焦點
為過焦點![]() 且垂直于
且垂直于![]() 軸的拋物線
軸的拋物線![]() 的弦,已知以
的弦,已知以![]() 為直徑的圓經(jīng)過點
為直徑的圓經(jīng)過點![]() .
.
(1)求![]() 的值及該圓的方程;
的值及該圓的方程;
(2)設![]() 為
為![]() 上任意一點,過點
上任意一點,過點![]() 作
作![]() 的切線,切點為
的切線,切點為![]() ,證明:
,證明:![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)f(x)=axlnx﹣x2﹣ax+1(a∈R)在定義域內(nèi)有兩個不同的極值點.
(1)求實數(shù)a的取值范圍;
(2)設兩個極值點分別為x1,x2,x1<x2,證明:f(x1)+f(x2)<2﹣x12+x22.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】為了貫徹落實黨中央對新冠肺炎疫情防控工作的部署和要求,堅決防范疫情向校園蔓延,切實保障廣大師生身體健康和生命的安全,教育主管部門決定通過電視頻道、網(wǎng)絡平臺等多種方式實施線上教育教學工作.為了了解學生和家長對網(wǎng)課授課方式的滿意度,從經(jīng)濟不發(fā)達的A城市和經(jīng)濟發(fā)達的B城市分別隨機調(diào)查了20個用戶,得到了一個用戶滿意度評分的樣本,并繪制出莖葉圖如下:
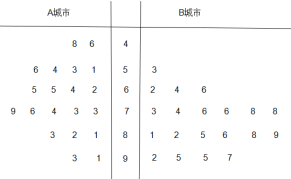
若評分不低于80分,則認為該用戶對此授課方式“認可”,否則認為該用戶對此授課方式“不認可”.以該樣本中A,B城市的用戶對此授課方式“認可”的頻率分別作為A,B城市用戶對此授課方式“認可”的概率.現(xiàn)從A城市和B城市的所有用戶中分別隨機抽取2個用戶,用![]() 表示這4個用戶中對此授課方式“認可”的用戶個數(shù),則
表示這4個用戶中對此授課方式“認可”的用戶個數(shù),則![]() __________;用
__________;用![]() 表示從A城市隨機抽取2個用戶中對此授課方式“認可”的用戶個數(shù),則
表示從A城市隨機抽取2個用戶中對此授課方式“認可”的用戶個數(shù),則![]() 的數(shù)學期望為_________ .
的數(shù)學期望為_________ .
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,已知橢圓C:![]() 過原點的直線與橢圓交于A,B兩點(點A在第一象限),過點A作x軸的垂線,垂足為點
過原點的直線與橢圓交于A,B兩點(點A在第一象限),過點A作x軸的垂線,垂足為點![]() ,設直線BE與橢圓的另一交點為P,連接AP得到直線l,交x軸于點M,交y軸于點N.
,設直線BE與橢圓的另一交點為P,連接AP得到直線l,交x軸于點M,交y軸于點N.
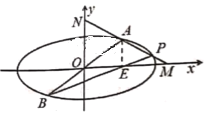
(1)若![]() ,求直線AP的斜率;
,求直線AP的斜率;
(2)記![]() 的面積分別為S1,S2,S3,求
的面積分別為S1,S2,S3,求![]() 的的最大值.
的的最大值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】設數(shù)列![]() 中前兩項
中前兩項![]() 給定,若對于每個正整數(shù)
給定,若對于每個正整數(shù)![]() ,均存在正整數(shù)
,均存在正整數(shù)![]() (
(![]() )使得
)使得![]() ,則稱數(shù)列
,則稱數(shù)列![]() 為“
為“![]() 數(shù)列”.
數(shù)列”.
(1)若數(shù)列![]() 為
為![]() 的等比數(shù)列,當
的等比數(shù)列,當![]() 時,試問:
時,試問:![]() 與
與![]() 是否相等,并說明數(shù)列
是否相等,并說明數(shù)列![]() 是否為“
是否為“![]() 數(shù)列”;
數(shù)列”;
(2)討論首項為![]() 、公差為
、公差為![]() 的等差數(shù)列
的等差數(shù)列![]() 是否為“
是否為“![]() 數(shù)列”,并說明理由;
數(shù)列”,并說明理由;
(3)已知數(shù)列![]() 為“
為“![]() 數(shù)列”,且
數(shù)列”,且![]() ,記
,記![]() ,
,![]() ,其中正整數(shù)
,其中正整數(shù)![]() , 對于每個正整數(shù)
, 對于每個正整數(shù)![]() ,當正整數(shù)
,當正整數(shù)![]() 分別取1、2、
分別取1、2、![]() 、
、![]() 時
時![]() 的最大值記為
的最大值記為![]() 、最小值記為
、最小值記為![]() . 設
. 設![]() ,當正整數(shù)
,當正整數(shù)![]() 滿足
滿足![]() 時,比較
時,比較![]() 與
與![]() 的大小,并求出
的大小,并求出![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)當![]() 時,求函數(shù)
時,求函數(shù)![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(2)設函數(shù)![]() ,若函數(shù)
,若函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上存在正的極值,求實數(shù)
上存在正的極值,求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】設n為正整數(shù),集合A=![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .對于集合A中的任意元素
.對于集合A中的任意元素![]() 和
和![]() ,記
,記![]() .
.
(Ⅰ)當n=3時,若![]() ,
,![]() ,求
,求![]() 和
和![]() 的值;
的值;
(Ⅱ)當![]() 時,對于
時,對于![]() 中的任意兩個不同的元素
中的任意兩個不同的元素![]() ,
,![]() ,證明:
,證明:![]() .
.
(Ⅲ)給定不小于2的正整數(shù)n,設B是A的子集,且滿足:對于B中的任意兩個不同元素![]() ,
,![]() ,
,![]() .寫出一個集合B,使其元素個數(shù)最多,并說明由.
.寫出一個集合B,使其元素個數(shù)最多,并說明由.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com