
【題目】已知數列{an}滿足a1=1,|an+1﹣an|=pn , n∈N* .
(1)若{an}是遞增數列,且a1 , 2a2 , 3a3成等差數列,求p的值;
(2)若p= ![]() ,且{a2n﹣1}是遞增數列,{a2n}是遞減數列,求數列{an}的通項公式.
,且{a2n﹣1}是遞增數列,{a2n}是遞減數列,求數列{an}的通項公式.
【答案】
(1)解:∵數列{an}是遞增數列,∴an+1﹣an>0,
則|an+1﹣an|=pn化為:an+1﹣an=pn,
分別令n=1,2可得,a2﹣a1=p, ![]() ,
,
即a2=1+p, ![]() ,
,
∵a1,2a2,3a3成等差數列,∴4a2=a1+3a3,
即4(1+p)=1+3(p2+p+1),
化簡得3p2﹣p=0,解得 ![]() 或0,
或0,
當p=0時,數列an為常數數列,不符合數列{an}是遞增數列,
∴ ![]() ;
;
(2)解:由題意可得,|an+1﹣an|= ![]() ,
,
則|a2n﹣a2n﹣1|= ![]() ,|a2n+2﹣a2n+1|=
,|a2n+2﹣a2n+1|= ![]() ,
,
∵數列{a2n﹣1}是遞增數列,且{a2n}是遞減數列,
∴a2n+1﹣a2n﹣1>0,且a2n+2﹣a2n<0,
則﹣(a2n+2﹣a2n)>0,兩不等式相加得
a2n+1﹣a2n﹣1﹣(a2n+2﹣a2n)>0,即a2n+1﹣a2n+2>a2n﹣1﹣a2n,
又∵|a2n﹣a2n﹣1|= ![]() >|a2n+2﹣a2n+1|=
>|a2n+2﹣a2n+1|= ![]() ,
,
∴a2n﹣a2n﹣1>0,即 ![]() ,
,
同理可得:a2n+3﹣a2n+2>a2n+1﹣a2n,即|a2n+3﹣a2n+2|<|a2n+1﹣a2n|,
則a2n+1﹣a2n= ![]()
當數列{an}的項數為偶數時,令n=2m(m∈N*),
![]() ,
, ![]() ,
, ![]() ,…,
,…, ![]() ,
,
這2m﹣1個等式相加可得, ![]()
= 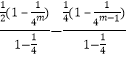 =
= ![]() ,
,
則 ![]() ;
;
當數列{an}的項數為奇數時,令n=2m+1(m∈N*)
![]() ,
, ![]() ,
, ![]() ,…,
,…, ![]() ,
,
這2m個等式相加可得, ![]()
= 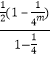 ﹣
﹣ 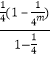 =
= ![]() ,
,
則 ![]() ,且當m=0時a1=1符合,
,且當m=0時a1=1符合,
故 ![]() ,
,
綜上得, 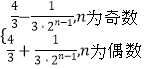
【解析】(1)根據條件去掉式子的絕對值,分別令n=1,2代入求出a2和a3 , 再由等差中項的性質列出關于p的方程求解,利用“{an}是遞增數列”對求出的p的值取舍;(2)根據數列的單調性和式子“|an+1﹣an|=pn”、不等式的可加性,求出 ![]() 和a2n+1﹣a2n=
和a2n+1﹣a2n= ![]() ,再對數列{an}的項數分類討論,利用累加法和等比數列前n項和公式,求出數列{an}的奇數項、偶數項對應的通項公式,再用分段函數的形式表示出來.
,再對數列{an}的項數分類討論,利用累加法和等比數列前n項和公式,求出數列{an}的奇數項、偶數項對應的通項公式,再用分段函數的形式表示出來.
【考點精析】利用數列的前n項和和數列的通項公式對題目進行判斷即可得到答案,需要熟知數列{an}的前n項和sn與通項an的關系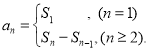 ;如果數列an的第n項與n之間的關系可以用一個公式表示,那么這個公式就叫這個數列的通項公式.
;如果數列an的第n項與n之間的關系可以用一個公式表示,那么這個公式就叫這個數列的通項公式.


科目:高中數學 來源: 題型:
【題目】2018年2月9-25日,第23屆冬奧會在韓國平昌舉行.4年后,第24 屆冬奧會將在中國北京和張家口舉行.為了宣傳冬奧會,某大學在平昌冬奧會開幕后的第二天,從全校學生中隨機抽取了120名學生,對是否收看平昌冬奧會開幕式情況進行了問卷調查,統計數據如下:

(1)根據上表說明,能否有![]() 的把握認為,收看開幕式與性別有關?
的把握認為,收看開幕式與性別有關?
(2)現從參與問卷調查且收看了開幕式的學生中,采用按性別分層抽樣的方法,選取12人參加2022年北京冬奧會志愿者宣傳活動.若從這12人中隨機選取3人到校廣播站開展冬奧會及冰雪項目的宣傳介紹,設選取的3 人中女生人數為![]() ,寫出
,寫出![]() 的分布列,并求
的分布列,并求![]() .
.
附:![]() ,其中
,其中![]() .
.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某企業有甲、乙兩個研發小組,他們研發新產品成功的概率分別為 ![]() 和
和 ![]() .現安排甲組研發新產品A,乙組研發新產品B,設甲、乙兩組的研發相互獨立.
.現安排甲組研發新產品A,乙組研發新產品B,設甲、乙兩組的研發相互獨立.
(1)求至少有一種新產品研發成功的概率;
(2)若新產品A研發成功,預計企業可獲利潤120萬元;若新產品B研發成功,預計企業可獲利潤100萬元,求該企業可獲利潤的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某班![]() 名同學的數學小測成績的頻率分布表如圖所示,其中
名同學的數學小測成績的頻率分布表如圖所示,其中![]() ,且分數在
,且分數在![]() 的有
的有![]() 人.
人.
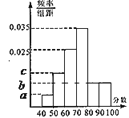
(1)求![]() 的值;
的值;
(2)若分數在![]() 的人數是分數在
的人數是分數在![]() 的人數的
的人數的![]() ,求從不及格的人中任意選取3人,其中分數在50分以下的人數為
,求從不及格的人中任意選取3人,其中分數在50分以下的人數為![]() ,求
,求![]() 的數學期.
的數學期.
查看答案和解析>>
科目:高中數學 來源: 題型:
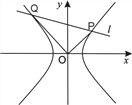
【題目】已知雙曲線![]() (b>a>0),O為坐標原點,離心率
(b>a>0),O為坐標原點,離心率![]() ,點
,點![]() 在雙曲線上.
在雙曲線上.
(1)求雙曲線的方程;
(2)若直線![]() 與雙曲線交于P、Q兩點,且
與雙曲線交于P、Q兩點,且![]() .求|OP|2+|OQ|2的最小值.
.求|OP|2+|OQ|2的最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com