
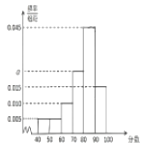
【題目】某學校為進一步規范校園管理,強化飲食安全,提出了“遠離外賣,健康飲食”的口號.當然,也需要學校食堂能提供安全豐富的菜品來滿足同學們的需求.在學期末,校學生會為了調研學生對本校食堂A部和B部的用餐滿意度,從在A部和B部都用過餐的學生中隨機抽取了200人,每人分別對其評分,滿分為100分.隨后整理評分數據,將分數分成6組:第1組![]() ,第2組
,第2組![]() ,第3組
,第3組![]() ,第4組
,第4組![]() ,第5組
,第5組![]() ,第6組
,第6組![]() ,得到A部分數的頻率分布直方圖和B部分數的頻數分布表.
,得到A部分數的頻率分布直方圖和B部分數的頻數分布表.
分數區間 | 頻數 |
| 7 |
| 18 |
| 21 |
| 24 |
| 70 |
| 60 |
定義:學生對食堂的“滿意度指數”
分數 |
|
|
|
|
|
|
滿意度指數 | 0 | 1 | 2 | 3 | 4 | 5 |
(1)求A部得分的中位數(精確到小數點后一位);
(2)A部為進一步改善經營,從打分在80分以下的前四組中,采用分層抽樣的方法抽取8人進行座談,再從這8人中隨機抽取3人參與“端午節包粽子”實踐活動,在第3組抽到1人的情況下,第4組抽到2人的概率;
(3)如果根據調研結果評選學生放心餐廳,應該評選A部還是B部(將頻率視為概率)
【答案】(1)82.2; (2)![]() ; (3)A部
; (3)A部
【解析】
(1)由頻率分布直方圖面積之和為![]() ,求得參數
,求得參數![]() ;再由頻率分布直方圖求中位數即可;
;再由頻率分布直方圖求中位數即可;
(2)根據分層抽樣,結合條件概率的求解,即可求得;
(3)先后求得![]() 的分布列和數學期望,即可容易判斷.
的分布列和數學期望,即可容易判斷.
(1)由![]() ,得
,得![]()
設A部得分的中位數為![]() ,
,
則![]() ,得
,得![]()
![]() 部得分的中位數為82.2
部得分的中位數為82.2
(2)第1,2,3,4組的人數分別為10,10,20,40,
從第1,2,3,4組采用分層抽樣方法抽取8,人,
則從第1,2,3,4組應分別抽取的人數為1,1,2,4.
從8人中抽取3人,記第3組抽到1人為事件A,第4組抽到2人為事件B.
則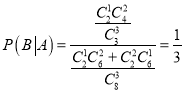 ,
,
即在第3組抽到1人的情況下,第4組抽到2人的概率為![]() .
.
(3)記對A部評價的滿意度指數為隨機變量X,則X的分布列為
X | 0 | 1 | 2 | 3 | 4 | 5 |
P | 0.05 | 0.05 | 0.1 | 0.2 | 0.45 | 0.15 |
![]()
記對B部評價的滿意度指數為隨機變量Y,則Y的分布列為
X | 0 | 1 | 2 | 3 | 4 | 5 |
P |
|
|
|
|
|
|
![]()
![]() ,故應該評選A部為學生放心餐廳.
,故應該評選A部為學生放心餐廳.


 通城學典默寫能手系列答案
通城學典默寫能手系列答案科目:高中數學 來源: 題型:
【題目】已知函數f(x)=log4(4x+1)+kx(k∈R)是偶函數.
(1)求k的值;
(2)設g(x)=log4![]() ,若函數f(x)與g(x)的圖象有且只有一個公共點,求實數a的取值范圍.
,若函數f(x)與g(x)的圖象有且只有一個公共點,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
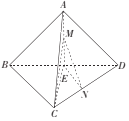
【題目】如圖,在三棱錐A﹣BCD中,點E在BD上,EA=EB=EC=ED,BD![]() CD,△ACD為正三角形,點M,N分別在AE,CD上運動(不含端點),且AM=CN,則當四面體C﹣EMN的體積取得最大值
CD,△ACD為正三角形,點M,N分別在AE,CD上運動(不含端點),且AM=CN,則當四面體C﹣EMN的體積取得最大值![]() 時,三棱錐A﹣BCD的外接球的表面積為_____.
時,三棱錐A﹣BCD的外接球的表面積為_____.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線![]() 的焦點為F,A為C上異于原點的任意一點,過點A的直線交y軸正半軸于點B,且有
的焦點為F,A為C上異于原點的任意一點,過點A的直線交y軸正半軸于點B,且有![]() ,當點A的縱坐標為6時,
,當點A的縱坐標為6時,![]() 為正三角形.
為正三角形.
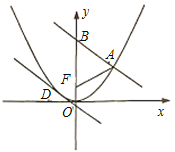
(1)求C的方程;
(2)若直線![]() ,且
,且![]() 和C有且只有一個公共點D,證明:直線AD過定點,并求出該定點坐標.
和C有且只有一個公共點D,證明:直線AD過定點,并求出該定點坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(1)若函數![]() 在
在![]() ,
,![]() 上單調遞增,求實數
上單調遞增,求實數![]() 的取值范圍;
的取值范圍;
(2)若函數![]() 在
在![]() 處的切線平行于
處的切線平行于![]() 軸,是否存在整數
軸,是否存在整數![]() ,使不等式
,使不等式![]() 在
在![]() 時恒成立?若存在,求出
時恒成立?若存在,求出![]() 的最大值;若不存在,請說明理由.
的最大值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平行四邊形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 是EA的中點(如圖1),將
是EA的中點(如圖1),將![]() 沿CD折起到圖2中
沿CD折起到圖2中![]() 的位置,得到四棱錐是
的位置,得到四棱錐是![]() .
.
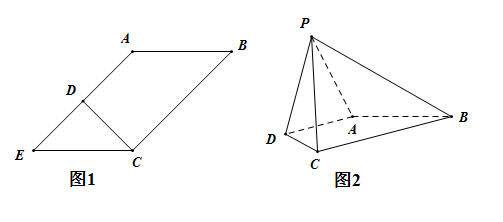
(1)求證:![]() 平面PDA;
平面PDA;
(2)若PD與平面ABCD所成的角為![]() .且
.且![]() 為銳角三角形,求平面PAD和平面PBC所成銳二面角的余弦值.
為銳角三角形,求平面PAD和平面PBC所成銳二面角的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線![]() 和
和![]() 軸上的定點
軸上的定點![]() ,過拋物線焦點作一條直線交
,過拋物線焦點作一條直線交![]() 于
于![]() 、
、![]() 兩點,連接
兩點,連接![]() 并延長,交
并延長,交![]() 于
于![]() 、
、![]() 兩點.
兩點.
(1)求證:直線![]() 過定點;
過定點;
(2)求直線![]() 與直線
與直線![]() 最大夾角為
最大夾角為![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,![]() 是正方形,點
是正方形,點![]() 在以
在以![]() 為直徑的半圓弧上(
為直徑的半圓弧上(![]() 不與
不與![]() ,
,![]() 重合),
重合),![]() 為線段
為線段![]() 的中點,現將正方形
的中點,現將正方形![]() 沿
沿![]() 折起,使得平面
折起,使得平面![]() 平面
平面![]() .
.

(1)證明:![]() 平面
平面![]() .
.
(2)若![]() ,當三棱錐
,當三棱錐![]() 的體積最大時,求
的體積最大時,求![]() 到平面
到平面![]() 的距離.
的距離.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了調節高三學生學習壓力,某校高三年級舉行了拔河比賽,在賽前三位老師對前三名進行了預測,于是有了以下對話:老師甲:“7班男生比較壯,7班肯定得第一名”.老師乙:“我覺得14班比15班強,14班名次會比15班靠前”.老師丙:“我覺得7班能贏15班”.最后老師丁去觀看完了比賽,回來后說:“確實是這三個班得了前三名,且無并列,但是你們三人中只有一人預測準確”.那么,獲得一、二、三名的班級依次為( )
A.7班、14班、15班B.14班、7班、15班
C.14班、15班、7班D.15班、14班、7班
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com