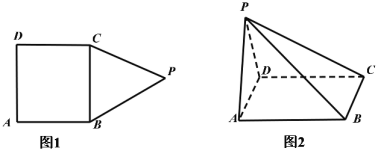
【題目】如圖，在多邊形
中（圖1）．四邊形
為長方形，
為正三角形，
，
，現以
為折痕將折起，使點
在平面內的射影恰好是
的中點（圖2）．
（1）證明：
平面
：
（2）若點
在線段
上，且
，求二面角
的余弦值．
科目：高中數學 來源： 題型：
【題目】已知曲線
上的點到
的距離比它到直線
的距離少3.
（1）求曲線的方程；
（2）過點
且斜率為
的直線
交曲線于
，
兩點，交圓
于
，
兩點，，在
軸上方，過點，分別作曲線的切線
，
，
，求
與
的面積的積的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
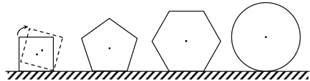
【題目】現有邊長均為1的正方形正五邊形正六邊形及半徑為1的圓各一個，在水平桌面上無滑動滾動一周，它們的中心的運動軌跡長分別為
，
，
，
，則（ ）
A.
B.
C.
D.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】過拋物線C：x2＝4y的準線上任意一點P作拋物線的切線PA，PB，切點分別為A，B，則A點到準線的距離與B點到準線的距離之和的最小值是（ ）
A.7B.6C.5D.4
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】2020年初，新型冠狀病毒肺炎（COVID－19）在我國爆發，全國人民團結一心、積極抗疫，為全世界疫情防控爭取了寶貴的時間，積累了豐富的經驗.某研究小組為了研究某城市肺炎感染人數的增長情況，在官方網站．上搜集了7組數據，并依據數據制成如下散點圖：
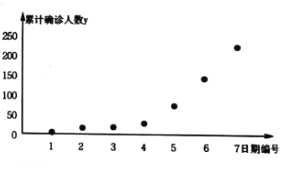
圖中
表示日期代號（例如2月1日記為“1”，2月2日記為“2”，以此類推）．通過對散點圖的分析，結合病毒傳播的相關知識，該研究小組決定用指數型函數模型
來擬合，為求出
關于的回歸方程，可令
，則
與線性相關．初步整理后，得到如下數據：
，
．
（1）根據所給數據，求出關于的線性回歸方程：
（2）求關于的回歸方程；若防控不當，請問為何值時，累計確診人數的預報值將超過1000人?（參考數據：
，結果保留整數）
附：對于一組數據
，其線性回歸方程
的斜率和截距的最小二乘估計公式分別為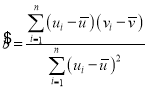
，
．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在直角坐標系
中，曲線
的參數方程為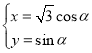
（
為參數），以原點
為極點，以
軸正半軸為極軸，建立極坐標系，曲線
的極坐標方程為
.
（1）求曲線的普通方程與曲線的直角坐標方程；
（2）設
為曲線上位于第一，二象限的兩個動點，且
，射線
交曲線分別于
，求
面積的最小值，并求此時四邊形
的面積.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，直線PQ與⊙O相切于點A，AB是⊙O的弦，∠PAB的平分線AC交⊙O于點C，連結CB，并延長與直線PQ相交于點Q，若AQ=6，AC=5．
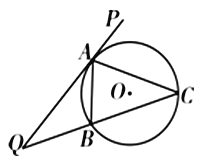
（Ⅰ）求證：QC2﹣QA2=BC
QC；
（Ⅱ）求弦AB的長．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
