Question

【題目】已知函數，．

（Ⅰ）若在上存在極大值點，求實數的取值范圍；

（Ⅱ）求證：，其中．

Answer 1

【答案】（Ⅰ） （Ⅱ）見證明

【解析】

（Ⅰ）先對函數求導，再由分類討論的思想，分別討論，和三種情況，即可得出結果；

（Ⅱ）令可得，由（Ⅰ）可知的極大值，再由時，，即可證明結論成立；也可用數學歸納法證明.

解：（Ⅰ）由于，

則①當時，，

即當時，，單調遞增；

當時，，單調遞減；

故在處取得極大值，

則，解得：；

②當時，恒成立，無極值，不合題意舍去；

③當時，，

即當時，，單調遞減；

當時， ，單調遞增；

故在處取得極小值，不合題意舍去；

因此當時，在上存在極大值點；

（Ⅱ）法一：令，，

由（Ⅰ）得：在處取得極大值1，且該極值是唯一的，

則，即，當且僅當時取“=”，

故當時，，

因此．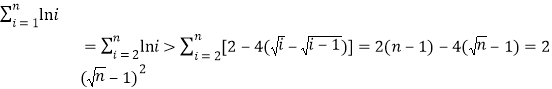

法二：下面用數學歸納法證明：，對恒成立．

（1）當時，左邊，右邊，

左邊右邊，結論成立；

（2）假設當時，結論成立，即，

當時，左邊

，

而 ，

令，，

由（Ⅰ）得：在處取得極大值1，且該極值是唯一的，

則，即，當且僅當時取“=”，

則對恒成立，即

成立

故當時，結論成立，

因此，綜合（1）（2）得，對恒成立