
【題目】如圖,四邊形ABCD是矩形,MD⊥平面ABCD,NB∥MD,且AD=2,NB=1,CD=MD=3.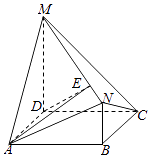
(1)過B作平面BFG∥平面MNC,平面BFG與CD、DM分別交于F、G,求AF與平面MNC所成角的正弦值;
(2)E為直線MN上一點,且平面ADE⊥平面MNC,求 ![]() 的值.
的值.
【答案】
(1)解:當CF=MG=1時,平面BFG∥平面MNC.
證明:連接BF,FG,GB,∵BN=GM=1,BN∥GM,∴四邊形BNMG是平行四邊形,∴BG∥NM,∵CD=MD,CF=MG,∴FG∥CM,∵BG∩FG=G,∴平面BFG∥平面MNC,
以D為原點,DA,DC,DM所在直線分別為x,y,z軸,建立空間直角坐標系(如圖),則A(2,0,0),C(0,3,0),F(0,2,0),M(0,0,3),N(2,3,1),∴ ![]() =(﹣2,2,0),
=(﹣2,2,0), ![]() =(2,3,﹣2),
=(2,3,﹣2), ![]() =(0,3,﹣3),
=(0,3,﹣3),
設平面MNC的一個法向量 ![]() =(x,y,z),
=(x,y,z),
則 ![]() 令y=2,則z=2,x=﹣1,∴
令y=2,則z=2,x=﹣1,∴ ![]() =(﹣1,2,2),
=(﹣1,2,2),
設AF與平面MNC所成角為θ,則 ![]()
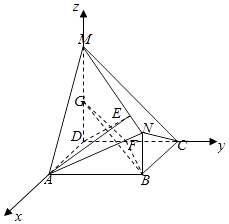
(2)解:設E(a,b,c), ![]() ,則
,則 ![]() =λ
=λ ![]() ,
,
∵ ![]() =(a,b,c﹣3),
=(a,b,c﹣3), ![]() =(2,3,﹣2),∴點E的坐標為(2λ,3λ,3﹣2λ),
=(2,3,﹣2),∴點E的坐標為(2λ,3λ,3﹣2λ),
∵AD⊥平面MDC,∴AD⊥MC,
欲使平面ADE⊥平面MNC,只要AE⊥MC,
∵ ![]() =(2λ﹣2,3λ,3﹣2λ),
=(2λ﹣2,3λ,3﹣2λ), ![]() =(0,3,﹣3),∴9λ﹣3(3﹣2λ)=0,得
=(0,3,﹣3),∴9λ﹣3(3﹣2λ)=0,得 ![]() ,∴
,∴ ![]() .
.
【解析】(1)先分析所給的條件,進而建立合適的空間直角坐標系,再利用向量法求AF與平面MNC所成角的正弦值;(2)根據“欲使平面ADE⊥平面MNC,只要AE⊥MC”的依據是:如果一個平面經過另一個平面的一條垂線,那么這兩個平面互相垂直.
【考點精析】利用平面與平面平行的判定和平面與平面垂直的判定對題目進行判斷即可得到答案,需要熟知判斷兩平面平行的方法有三種:用定義;判定定理;垂直于同一條直線的兩個平面平行;一個平面過另一個平面的垂線,則這兩個平面垂直.


科目:高中數學 來源: 題型:
【題目】已知橢圓C的中心在原點,一個焦點F(﹣2,0),且長軸長與短軸長的比是 ![]() .
.
(1)求橢圓C的方程;
(2)設點M(m,0)在橢圓C的長軸上,點P是橢圓上任意一點.當 ![]() 最小時,點P恰好落在橢圓的右頂點,求實數m的取值范圍.
最小時,點P恰好落在橢圓的右頂點,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某企業為了解下屬某部門對本企業職工的服務情況,隨機訪問50名職工,根據這50名職工對該部門的評分,繪制頻率分布直方圖(如圖所示),其中樣本數據分組區間為![]()

(1)求頻率分布圖中![]() 的值,并估計該企業的職工對該部門評分不低于80的概率;
的值,并估計該企業的職工對該部門評分不低于80的概率;
(2)從評分在![]() 的受訪職工中,隨機抽取2人,求此2人評分都在
的受訪職工中,隨機抽取2人,求此2人評分都在![]() 的概率..
的概率..
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在正方體ABCD﹣A1B1C1D1中,E是A1B1上一點,若平面EBD與平面ABCD所成銳二面角的正切值為 ![]() ,設三棱錐A﹣A1D1E外接球的直徑為a,則
,設三棱錐A﹣A1D1E外接球的直徑為a,則 ![]() = .
= .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,
, ![]() ,設
,設![]() (其中
(其中![]() 表示
表示![]() 中的較小者).
中的較小者).
(1)在坐標系中畫出函數![]() 的圖像;
的圖像;
(2)設函數![]() 的最大值為
的最大值為![]() ,試判斷
,試判斷![]() 與1的大小關系,并說明理由.
與1的大小關系,并說明理由.
(參考數據: ![]() ,
, ![]() ,
, ![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】三棱錐A﹣BCD的所有棱長均為6,點P在AC上,且AP=2PC,過P作四面體的截面,使截面平行于直線AB和CD,則該截面的周長為( )
A.16
B.12
C.10
D.8
查看答案和解析>>
科目:高中數學 來源: 題型:
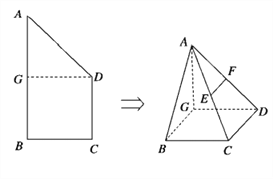
【題目】如圖,在直角梯形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 為線段
為線段![]() 的中點,將
的中點,將![]() 沿
沿![]() 折起,使平面
折起,使平面![]() 平面
平面![]() ,得到幾何體
,得到幾何體![]() .
.
(1)若![]() 分別為線段
分別為線段![]() 的中點,求證:
的中點,求證: ![]() 平面
平面![]() ;
;
(2)求證: ![]() 平面
平面![]() ;
;
(3)求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了普及環保知識,增強環保意識,某校從理科甲班抽取60人,從文科乙班抽取50人參加環保知識測試.
(Ⅰ)根據題目條件完成下面2×2列聯表,并據此判斷是否有99%的把握認為環保知識成績優秀與學生的文理分類有關.
優秀人數 | 非優秀人數 | 總計 | |
甲班 | |||
乙班 | 30 | ||
總計 | 60 |
(Ⅱ)現已知A,B,C三人獲得優秀的概率分別為 ![]() ,設隨機變量X表示A,B,C三人中獲得優秀的人數,求X的分布列及期望E(X).
,設隨機變量X表示A,B,C三人中獲得優秀的人數,求X的分布列及期望E(X).
附: ![]() ,n=a+b+c+d
,n=a+b+c+d
P(K2>k0) | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com