
【題目】已知函數(shù)![]()
(Ⅰ)當(dāng)a=﹣2時(shí),求函數(shù)f(x)的單調(diào)區(qū)間;
(Ⅱ)若g(x)= ![]() +
+![]() 在
在![]() 1,+∞)上是單調(diào)函數(shù),求實(shí)數(shù)a的取值范圍.
1,+∞)上是單調(diào)函數(shù),求實(shí)數(shù)a的取值范圍.
【答案】(Ⅰ)![]() 的單調(diào)遞增區(qū)間是(1,+∞),
的單調(diào)遞增區(qū)間是(1,+∞), ![]() 的單調(diào)遞減區(qū)間是(0, 1).
的單調(diào)遞減區(qū)間是(0, 1).
(Ⅱ)實(shí)數(shù)a的取值范圍![]() 0,+∞)
0,+∞)
【解析】試題分析:(Ⅰ)求導(dǎo)函數(shù),利用導(dǎo)數(shù)的正負(fù),可得函數(shù)的單調(diào)遞增區(qū)間與單調(diào)遞減區(qū)間;(Ⅱ)由題意得![]() ,分函數(shù)g(x)為[1,+∞)上的單調(diào)增函數(shù)與單調(diào)減函數(shù)討論,即可確定實(shí)數(shù)a的取值范圍
,分函數(shù)g(x)為[1,+∞)上的單調(diào)增函數(shù)與單調(diào)減函數(shù)討論,即可確定實(shí)數(shù)a的取值范圍
試題解析:(1)由已知,函數(shù)的定義域?yàn)?/span>(0,+∞).
當(dāng)a=-2時(shí),f(x)=x2-2lnx,所以f′(x)=2x-![]() =
=![]() ,
,
則當(dāng)x∈(0,1)時(shí),f′(x)<0,所以(0,1)為f(x)的單調(diào)遞減區(qū)間.
當(dāng)x∈(1,+∞)時(shí),f′(x)>0,(1,+∞)為f(x)的單調(diào)遞增區(qū)間.
(2)由題意得g′(x)=2x+![]() -
-![]() ,函數(shù)g(x)在[1,+∞)上是單調(diào)函數(shù).
,函數(shù)g(x)在[1,+∞)上是單調(diào)函數(shù).
(ⅰ)若函數(shù)g(x)為[1,+∞)上的單調(diào)增函數(shù),
則g′(x)≥0在[1,+∞)上恒成立,即a≥![]() -2x2在[1,+∞)上恒成立,
-2x2在[1,+∞)上恒成立,
設(shè)φ(x)=![]() -2x2,因?yàn)?/span>φ(x)在[1,+∞]上單調(diào)遞減,
-2x2,因?yàn)?/span>φ(x)在[1,+∞]上單調(diào)遞減,
所以φ(x)max=φ(1)=0,所以a≥0.
(ⅱ)若函數(shù)g(x)為[1,+∞)上的單調(diào)減函數(shù),則g′(x)≤0在[1,+∞)上恒成立,不可能.
綜上,實(shí)數(shù)a的取值范圍是[0,+∞).


 閱讀快車系列答案
閱讀快車系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知![]() 為拋物線
為拋物線![]() :
: ![]() (
(![]() )的焦點(diǎn),直線
)的焦點(diǎn),直線![]() :
: ![]() 交拋物線
交拋物線![]() 于
于![]() ,
, ![]() 兩點(diǎn).
兩點(diǎn).
(Ⅰ)當(dāng)![]() ,
, ![]() 時(shí),求拋物線
時(shí),求拋物線![]() 的方程;
的方程;
(Ⅱ)過(guò)點(diǎn)![]() ,
, ![]() 作拋物線
作拋物線![]() 的切線,
的切線, ![]() ,
, ![]() 交點(diǎn)為
交點(diǎn)為![]() ,若直線
,若直線![]() 與直線
與直線![]() 斜率之和為
斜率之和為![]() ,求直線
,求直線![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】某中學(xué)一位高三班主任對(duì)本班50名學(xué)生學(xué)習(xí)積極性和對(duì)待班級(jí)工作的態(tài)度進(jìn)行調(diào)查,得到的統(tǒng)計(jì)數(shù)據(jù)如下表所示:
積極參加班級(jí)工作 | 不積極參加班級(jí)工作 | 合計(jì) | |
學(xué)習(xí)積極性高 | 18 | 7 | 25 |
學(xué)習(xí)積極性不高 | 6 | 19 | 25 |
合計(jì) | 24 | 26 | 50 |
(1)如果隨機(jī)調(diào)查這個(gè)班的一名學(xué)生,那么抽到不積極參加班級(jí)工作且學(xué)習(xí)積極性不高的學(xué)生的概率是多少?
(2)若不積極參加班級(jí)工作且學(xué)習(xí)積極性高的7名學(xué)生中有兩名男生,現(xiàn)從中抽取兩名學(xué)生參加某項(xiàng)活動(dòng),問(wèn)兩名學(xué)生中有1名男生的概率是多少?
(3)學(xué)生的學(xué)習(xí)積極性與對(duì)待班極工作的態(tài)度是否有關(guān)系?請(qǐng)說(shuō)明理由.
附:
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
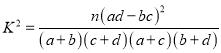
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】某高校大一新生中的6名同學(xué)打算參加學(xué)校組織的“雅荷文學(xué)社”、“青春風(fēng)街舞社”、“羽乒協(xié)會(huì)”、“演講團(tuán)”、“吉他協(xié)會(huì)”五個(gè)社團(tuán),若每名同學(xué)必須參加且只能參加1個(gè)社團(tuán)且每個(gè)社團(tuán)至多兩人參加,則這6個(gè)人中至多有1人參加“演講團(tuán)”的不同參加方法數(shù)為( )
A. 4680 B. 4770 C. 5040 D. 5200
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】某單位需要從甲、乙![]() 人中選拔一人參加新崗位培訓(xùn),特別組織了
人中選拔一人參加新崗位培訓(xùn),特別組織了![]() 個(gè)專項(xiàng)的考試,成績(jī)統(tǒng)計(jì)如下:
個(gè)專項(xiàng)的考試,成績(jī)統(tǒng)計(jì)如下:
第一項(xiàng) | 第二項(xiàng) | 第三項(xiàng) | 第四項(xiàng) | 第五項(xiàng) | |
甲的成績(jī) |
|
|
|
|
|
乙的成績(jī) |
|
|
|
|
|
(1)根據(jù)有關(guān)統(tǒng)計(jì)知識(shí),回答問(wèn)題:若從甲、乙![]() 人中選出
人中選出![]() 人參加新崗培訓(xùn),你認(rèn)為選誰(shuí)合適,請(qǐng)說(shuō)明理由;
人參加新崗培訓(xùn),你認(rèn)為選誰(shuí)合適,請(qǐng)說(shuō)明理由;
(2)根據(jù)有關(guān)槪率知識(shí),解答以下問(wèn)題:
從甲、乙![]() 人的成績(jī)中各隨機(jī)抽取一個(gè),設(shè)抽到甲的成績(jī)?yōu)?/span>
人的成績(jī)中各隨機(jī)抽取一個(gè),設(shè)抽到甲的成績(jī)?yōu)?/span>![]() ,抽到乙的成績(jī)?yōu)?/span>
,抽到乙的成績(jī)?yōu)?/span>![]() ,用
,用![]() 表示滿足條件
表示滿足條件![]() 的事件,求事件
的事件,求事件![]() 的概率.
的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]() 是自然對(duì)數(shù)的底數(shù).
是自然對(duì)數(shù)的底數(shù).
(1)討論函數(shù)![]() 在
在![]() 上的單調(diào)性;
上的單調(diào)性;
(2)當(dāng)![]() 時(shí),若存在
時(shí),若存在![]() ,使得
,使得![]() ,求實(shí)數(shù)
,求實(shí)數(shù)![]() 的取值范圍.(參考公式:
的取值范圍.(參考公式:![]() )
)
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]() .
.
(1)求![]() 在
在![]() 上的最小值
上的最小值![]() ;
;
(2)若存在兩個(gè)不同的實(shí)數(shù)![]() ,使得
,使得![]() ,求證:
,求證:![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知橢圓![]() :
:![]() (
(![]() )的離心率為
)的離心率為![]() ,連接橢圓的四個(gè)頂點(diǎn)得到的四邊形的面積為
,連接橢圓的四個(gè)頂點(diǎn)得到的四邊形的面積為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)設(shè)橢圓![]() 的左焦點(diǎn)為
的左焦點(diǎn)為![]() ,右焦點(diǎn)為
,右焦點(diǎn)為![]() ,直線
,直線![]() 過(guò)點(diǎn)
過(guò)點(diǎn)![]() 且垂直于橢圓的長(zhǎng)軸,動(dòng)直線
且垂直于橢圓的長(zhǎng)軸,動(dòng)直線![]() 垂直
垂直![]() 于點(diǎn)
于點(diǎn)![]() ,線段
,線段![]() 的垂直平分線交
的垂直平分線交![]() 于點(diǎn)
于點(diǎn)![]() ,求點(diǎn)
,求點(diǎn)![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(3)設(shè)![]() 為坐標(biāo)原點(diǎn),取
為坐標(biāo)原點(diǎn),取![]() 上不同于
上不同于![]() 的點(diǎn)
的點(diǎn)![]() ,以
,以![]() 為直徑作圓與
為直徑作圓與![]() 相交另外一點(diǎn)
相交另外一點(diǎn)![]() ,求該圓面積的最小值時(shí)點(diǎn)
,求該圓面積的最小值時(shí)點(diǎn)![]() 的坐標(biāo).
的坐標(biāo).
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com