
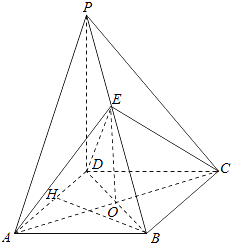
【題目】如圖,在四棱錐P﹣ABCD中,PD⊥平面ABCD,底面ABCD是菱形,∠BAD=60°,AB=2,PD= ![]() ,O為AC與BD的交點,E為棱PB上一點.
,O為AC與BD的交點,E為棱PB上一點. 
(Ⅰ)證明:平面EAC⊥平面PBD;
(Ⅱ)若PD∥平面EAC,求三棱錐P﹣EAD的體積.
【答案】(Ⅰ)證明:∵PD⊥平面ABCD,AC平面ABCD, ∴AC⊥PD.∵四邊形ABCD是菱形,∴AC⊥BD,
又∵PD∩BD=D,AC⊥平面PBD.
而AC平面EAC,∴平面EAC⊥平面PBD.
(Ⅱ)解:∵PD∥平面EAC,平面EAC∩平面PBD=OE,
∴PD∥OE,
∵O是BD中點,∴E是PB中點.
取AD中點H,連結BH,∵四邊形ABCD是菱形,∠BAD=60°,
∴BH⊥AD,又BH⊥PD,AD∩PD=D,∴BD⊥平面PAD, ![]() .
.
∴ ![]()
= ![]() =
= ![]() .
.
【解析】(Ⅰ)由已知得AC⊥PD,AC⊥BD,由此能證明平面EAC⊥平面PBD.(Ⅱ)由已知得PD∥OE,取AD中點H,連結BH,由此利用 ![]() ,能求出三棱錐P﹣EAD的體積.
,能求出三棱錐P﹣EAD的體積.


科目:高中數學 來源: 題型:
【題目】設函數f(x)=|x﹣4|,g(x)=|2x+1|.
(1)解不等式f(x)<g(x);
(2)若2f(x)+g(x)>ax對任意的實數x恒成立,求a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=|x﹣1|﹣|x+2|. (Ⅰ)求不等式﹣2<f(x)<0的解集A;
(Ⅱ)若m,n∈A,證明:|1﹣4mn|>2|m﹣n|.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】函數f(x)=xln(ax+1)(a≠0).
(Ⅰ)討論f(x)的單調性;
(Ⅱ)若a>0且滿足:對x1 , x2∈[﹣1,1],都有|f(x1)﹣f(x2)|≤ln3﹣ln2,試比較ea﹣1與 ![]() 的大小,并證明.
的大小,并證明.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】函數f(x)=x3+x,x∈R,當 ![]() 時,f(msinθ)+f(1﹣m)>0恒成立,則實數m的取值范圍是( )
時,f(msinθ)+f(1﹣m)>0恒成立,則實數m的取值范圍是( )
A.(0,1)
B.(﹣∞,0)
C.![]()
D.(﹣∞,1)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一盒中裝有9張各寫有一個數字的卡片,其中4張卡片上的數字是1,3張卡片上的數字是2,2張卡片上的數字是3,從盒中任取3張卡片.
(1)求所取3張卡片上的數字完全相同的概率;
(2)![]() 表示所取3張卡片上的數字的中位數,求
表示所取3張卡片上的數字的中位數,求![]() 的分布列與數學期望.
的分布列與數學期望.
(注:若三個數![]() 滿足
滿足![]() ,則稱
,則稱![]() 為這三個數的中位數).
為這三個數的中位數).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=|x﹣1|+|x+a|﹣x﹣2. (Ⅰ)當a=1時,求不等式f(x)>0的解集;
(Ⅱ)設a>﹣1,且存在x0∈[﹣a,1),使得f(x0)≤0,求a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在某校矩形的航天知識競賽中,參與競賽的文科生與理科生人數之比為1:3,且成績分布在![]() 范圍內,規定分數在80以上(含80)的同學獲獎,按文理科用分層抽樣的放發抽取200人的成績作為樣本,得到成績的頻率分布直方圖.
范圍內,規定分數在80以上(含80)的同學獲獎,按文理科用分層抽樣的放發抽取200人的成績作為樣本,得到成績的頻率分布直方圖.
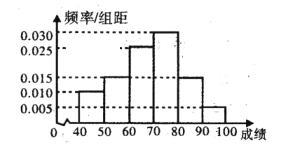
(Ⅰ)填寫下面![]() 的列聯表,能否有超過95%的把握認為“獲獎與學生的文理科有關”;
的列聯表,能否有超過95%的把握認為“獲獎與學生的文理科有關”;
(Ⅱ)將上述調查所得的頻率視為概率,現從參賽學生中,任意抽取3名學生,記“獲獎”學生人數為![]() ,求
,求![]() 的分布列及數學期望.
的分布列及數學期望.

附表及公式:![]() ,其中
,其中![]()

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an}的前n項和為Sn,且a1=1,an+1=![]() Sn(n=1,2,3,…).
Sn(n=1,2,3,…).
(1)求數列{an}的通項公式;
(2)當bn=![]() (3an+1)時,求證:數列
(3an+1)時,求證:數列![]() 的前n項和Tn=
的前n項和Tn=![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com