
【題目】△ABC的內(nèi)角A,B,C所對應(yīng)的邊分別為a,b,c.
(1)若a,b,c成等差數(shù)列,證明:sinA+sinC=2sin(A+C);
(2)若a,b,c成等比數(shù)列,求cosB的最小值.
【答案】
(1)解:∵a,b,c成等差數(shù)列,
∴2b=a+c,
利用正弦定理化簡得:2sinB=sinA+sinC,
∵sinB=sin[π﹣(A+C)]=sin(A+C),
∴sinA+sinC=2sinB=2sin(A+C);
(2)解:∵a,b,c成等比數(shù)列,
∴b2=ac,
∴cosB= ![]() =
= ![]() ≥
≥ ![]() =
= ![]() ,
,
當且僅當a=c時等號成立,
∴cosB的最小值為 ![]()
【解析】(1)由a,b,c成等差數(shù)列,利用等差數(shù)列的性質(zhì)列出關(guān)系式,利用正弦定理化簡,再利用誘導公式變形即可得證;(2)由a,bc成等比數(shù)列,利用等比數(shù)列的性質(zhì)列出關(guān)系式,再利用余弦定理表示出cosB,將得出的關(guān)系式代入,并利用基本不等式變形即可確定出cosB的最小值.


科目:高中數(shù)學 來源: 題型:
【題目】如圖所示,![]() 是海面上一條南北方向的海防警戒線,在
是海面上一條南北方向的海防警戒線,在 ![]() 上點
上點 ![]() 處有一個水聲監(jiān)測點,另兩個監(jiān)測點
處有一個水聲監(jiān)測點,另兩個監(jiān)測點 ![]() 分別在
分別在 ![]() 的正東方向
的正東方向 ![]() 處和
處和 ![]() 處.某時刻,監(jiān)測點
處.某時刻,監(jiān)測點 ![]() 收到發(fā)自目標
收到發(fā)自目標 ![]() 的一個聲波,
的一個聲波,![]() 后監(jiān)測點
后監(jiān)測點 ![]() 后監(jiān)測點
后監(jiān)測點 ![]() 相繼收到這一信號,在當時的氣象條件下,聲波在水中的傳播速度是
相繼收到這一信號,在當時的氣象條件下,聲波在水中的傳播速度是 ![]() .
.

(1)設(shè) ![]() 到
到 ![]() 的距離為
的距離為 ![]() ,用
,用 ![]() 分別表示
分別表示 ![]() 到
到 ![]() 的距離,并求
的距離,并求 ![]() 的值;
的值;
(2)求目標 ![]() 的海防警戒線
的海防警戒線 ![]() 的距離(精確到
的距離(精確到 ![]() ).
).
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在一段時間內(nèi),分5次測得某種商品的價格x(萬元)和需求量y(t)之間的一組數(shù)據(jù)為:
1 | 2 | 3 | 4 | 5 | |
價格x | 1.4 | 1.6 | 1.8 | 2 | 2.2 |
需求量y | 12 | 10 | 7 | 5 | 3 |
已知![]() ,
,
(1)畫出散點圖;
(2)求出y對x的線性回歸方程;
(3)如價格定為1.9萬元,預(yù)測需求量大約是多少?(精確到0.01 t).
參考公式: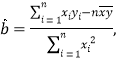
![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知橢圓![]() 的長軸長為4,直線
的長軸長為4,直線![]() 被橢圓
被橢圓![]() 截得的線段長為
截得的線段長為![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)過橢圓![]() 的右頂點作互相垂直的兩條直線
的右頂點作互相垂直的兩條直線![]() 分別交橢圓
分別交橢圓![]() 于
于![]() 兩點(點
兩點(點![]() 不同于橢圓
不同于橢圓![]() 的右頂點),證明:直線
的右頂點),證明:直線![]() 過定點
過定點![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】為了及時向群眾宣傳“十九大”黨和國家“鄉(xiāng)村振興”戰(zhàn)略,需要尋找一個宣講站,讓群眾能在最短的時間內(nèi)到宣講站.設(shè)有三個鄉(xiāng)鎮(zhèn),分別位于一個矩形![]() 的兩個頂點
的兩個頂點![]() 及
及![]() 的中點
的中點![]() 處,
處,![]() ,
,![]() ,現(xiàn)要在該矩形的區(qū)域內(nèi)(含邊界),且與
,現(xiàn)要在該矩形的區(qū)域內(nèi)(含邊界),且與![]() 等距離的一點
等距離的一點![]() 處設(shè)一個宣講站,記
處設(shè)一個宣講站,記![]() 點到三個鄉(xiāng)鎮(zhèn)的距離之和為
點到三個鄉(xiāng)鎮(zhèn)的距離之和為![]() .
.
(Ⅰ)設(shè)![]() ,將
,將![]() 表示為
表示為![]() 的函數(shù);
的函數(shù);
(Ⅱ)試利用(Ⅰ)的函數(shù)關(guān)系式確定宣講站![]() 的位置,使宣講站
的位置,使宣講站![]() 到三個鄉(xiāng)鎮(zhèn)的距離之和
到三個鄉(xiāng)鎮(zhèn)的距離之和![]() 最小.
最小.

查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某公司為確定下一年度投入某種產(chǎn)品的宣傳費,需了解年宣傳費![]() (單位:萬元)對年銷售量
(單位:萬元)對年銷售量![]() (單位:噸)和年利潤
(單位:噸)和年利潤![]() (單位:萬元)的影響.對近六年的年宣傳費
(單位:萬元)的影響.對近六年的年宣傳費![]() 和年銷售量
和年銷售量![]() 的數(shù)據(jù)作了初步統(tǒng)計,得到如下數(shù)據(jù):
的數(shù)據(jù)作了初步統(tǒng)計,得到如下數(shù)據(jù):
年份 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 |
年宣傳費 | 38 | 48 | 58 | 68 | 78 | 88 |
年銷售量 | 16.8 | 18.8 | 20.7 | 22.4 | 24.0 | 25.5 |
經(jīng)電腦模擬,發(fā)現(xiàn)年宣傳費![]() (萬元)與年銷售量
(萬元)與年銷售量![]() (噸)之間近似滿足關(guān)系式
(噸)之間近似滿足關(guān)系式![]() ,即
,即![]() .對上述數(shù)據(jù)作了初步處理,得到相關(guān)的值如下表:
.對上述數(shù)據(jù)作了初步處理,得到相關(guān)的值如下表:
|
|
|
|
75.3 | 24.6 | 18.3 | 101.4 |
(1)根據(jù)所給數(shù)據(jù),求![]() 關(guān)于
關(guān)于![]() 的回歸方程;
的回歸方程;
(2)規(guī)定當產(chǎn)品的年銷售量![]() (噸)與年宣傳費
(噸)與年宣傳費![]() (萬元)的比值在區(qū)間
(萬元)的比值在區(qū)間![]() 內(nèi)時認為該年效益良好.該公司某
內(nèi)時認為該年效益良好.該公司某![]() 年投入的宣傳費用(單位:萬元)分別為:
年投入的宣傳費用(單位:萬元)分別為:![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,試根據(jù)回歸方程估計年銷售量,從這
,試根據(jù)回歸方程估計年銷售量,從這![]() 年中任選
年中任選![]() 年,記其中選到效益良好年的數(shù)量為
年,記其中選到效益良好年的數(shù)量為![]() ,試求隨機變量
,試求隨機變量![]() 的分布列和期望.(其中
的分布列和期望.(其中![]() 為自然對數(shù)的底數(shù),
為自然對數(shù)的底數(shù),![]() )
)
附:對于一組數(shù)據(jù)![]() ,
,![]() ,…,
,…,![]() ,其回歸直線
,其回歸直線![]() 中的斜率和截距的最小二乘估計分別為
中的斜率和截距的最小二乘估計分別為 ,
,![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知A(2,2),B(5,3),C(3,-1).
(1)求△ABC的外接圓的方程;
(2)若點M(a,2)在△ABC的外接圓上,求a的值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】一個袋中裝有四個形狀大小完全相同的球,球的編號分別為1,2,3,4.
(1)從袋中隨機取兩個球,求取出的球的編號之和不大于4的概率;
(2)先從袋中隨機取一個球,該球的編號為m,將球放回袋中,然后再從袋中隨機取一個球,求n≥m+2的概率.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com