
【題目】已知橢圓![]() 的中心的中心在中心在坐標原點,焦點在
的中心的中心在中心在坐標原點,焦點在![]() 軸上且過點
軸上且過點![]() ,離心率是
,離心率是![]() .
.
(![]() )求橢圓
)求橢圓![]() 的標準方程.
的標準方程.
(![]() )直線
)直線![]() 過點
過點![]() 且與橢圓
且與橢圓![]() 交于
交于![]() 、
、![]() 兩點,若
兩點,若![]() ,求直線
,求直線![]() 的方程.
的方程.
 暑假作業海燕出版社系列答案
暑假作業海燕出版社系列答案 本土教輔贏在暑假高效假期總復習云南科技出版社系列答案
本土教輔贏在暑假高效假期總復習云南科技出版社系列答案 暑假作業北京藝術與科學電子出版社系列答案
暑假作業北京藝術與科學電子出版社系列答案科目:高中數學 來源: 題型:
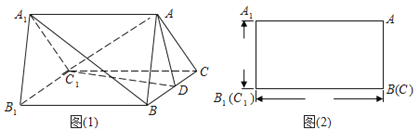
【題目】如圖(1)是一個水平放置的正三棱柱![]() ,
, ![]() 是棱
是棱![]() 的中點.正三棱柱的正(主)視圖如圖(2).
的中點.正三棱柱的正(主)視圖如圖(2).
(Ⅰ)求正三棱柱![]() 的體積;
的體積;
(Ⅱ)證明: ![]() ;
;
(Ⅲ)圖(1)中垂直于平面![]() 的平面有哪幾個?(直接寫出符合要求的平面即可,不必說明或證明)
的平面有哪幾個?(直接寫出符合要求的平面即可,不必說明或證明)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的左焦點
的左焦點![]() 與拋物線
與拋物線![]() 的焦點重合,橢圓
的焦點重合,橢圓![]() 的離心率為
的離心率為![]() ,過點
,過點![]() 作斜率不為0的直線
作斜率不為0的直線![]() ,交橢圓
,交橢圓![]() 于
于![]() 兩點,點
兩點,點![]() ,且
,且![]() 為定值.
為定值.
(1)求橢圓![]() 的方程;
的方程;
(2)求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某市準備引進優秀企業進行城市建設. 城市的甲地、乙地分別對5個企業(共10個企業)進行綜合評估,得分情況如莖葉圖所示.

(Ⅰ)根據莖葉圖,求乙地對企業評估得分的平均值和方差;
(Ⅱ)規定得分在85分以上為優秀企業. 若從甲、乙兩地準備引進的優秀企業中各隨機選取1個,求這兩個企業得分的差的絕對值不超過5分的概率.
注:方差![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的左右焦點分別為
的左右焦點分別為![]() , 若橢圓上一點
, 若橢圓上一點![]() 滿足
滿足![]() ,且橢圓
,且橢圓![]() 過點
過點![]() ,過點
,過點![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 交于兩點
交于兩點![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)若點![]() 是點
是點![]() 在
在![]() 軸上的垂足,延長
軸上的垂足,延長![]() 交橢圓
交橢圓![]() 于
于![]() ,求證:
,求證: ![]() 三點共線.
三點共線.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】【選修4-4:坐標系與參數方程】
極坐標系的極點為直角坐標系![]() 的原點,極軸為
的原點,極軸為![]() 軸的正半軸,兩神坐標系中的長度單位相同.已知曲線
軸的正半軸,兩神坐標系中的長度單位相同.已知曲線![]() 的極坐標方程為
的極坐標方程為![]() ,
, ![]() .
.
(Ⅰ)求曲線![]() 的直角坐標方程;
的直角坐標方程;
(Ⅱ)在曲線![]() 上求一點,使它到直線
上求一點,使它到直線![]() :
:  (
(![]() 為參數)的距離最短,寫出
為參數)的距離最短,寫出![]() 點的直角坐標.
點的直角坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com