
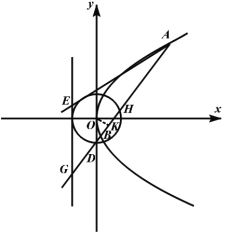
【題目】如圖,在平面直角系![]() 中,點A為曲線C:
中,點A為曲線C:![]() 在第一象限的圖象上的動點,點E,G在曲線C的準線
在第一象限的圖象上的動點,點E,G在曲線C的準線![]() 上,且點G在x軸的下方,圓O與準線相切,直線
上,且點G在x軸的下方,圓O與準線相切,直線![]() 交曲線C于點B,交圓O于點D,H.
交曲線C于點B,交圓O于點D,H.
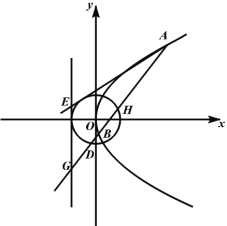
(1)當點H為曲線C的焦點,![]() 時,求
時,求![]() ;
;
(2)當點O為![]() 的內心時,若
的內心時,若![]() ,求點A的坐標.
,求點A的坐標.
【答案】(1)8;(2)![]() .
.
【解析】
(1)首先由準線方程可得拋物線方程,根據圓的弦長可得直線AG的方程,聯立直線AG與拋物線,結合焦半徑公式即可求解;(2)根據直線AE,AG與圓相切,結合圓心到直線的距離等于半徑,構造二次方程![]() 的兩根為
的兩根為![]() ,結合韋達定理即可建立等量關系,可求出點A的坐標.
,結合韋達定理即可建立等量關系,可求出點A的坐標.
(1)∵曲線C的準線為![]() ,∴
,∴![]() ,即
,即![]() ,
,
∴曲線C的方程為![]() .
.
∴此時![]() ,即
,即![]() .
.
過點O作![]() 于點K,則點K為弦
于點K,則點K為弦![]() 的中點.
的中點.
∵![]() ,∴
,∴![]() .
.
在![]() 中,
中,![]() ,
,
∴![]() ,即直線
,即直線![]() 的斜率為1,
的斜率為1,
∴直線![]() 的方程為
的方程為![]() .
.
設點![]() ,
,![]() .
.
聯立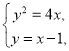 消去y,
消去y,
得![]() ,
,
由韋達定理得![]() ,
,
∴![]() .
.
(2)當點O為![]() 的內心時,點D與點H重合,即直線
的內心時,點D與點H重合,即直線![]() 與圓O相切.
與圓O相切.
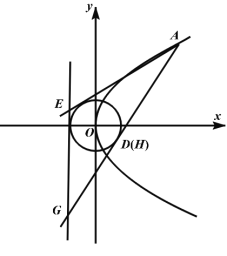
設![]() ,
,![]() ,
,![]() ,易知
,易知![]() ,
,![]() ,
,![]() .
.
直線![]() 的方程為
的方程為![]() ,
,
化簡得![]() .
.
又圓心![]() 到
到![]() 的距離為1,
的距離為1,
即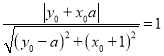 ,
,
∴![]() ,
,
化簡得![]() ,
,
同理有![]() .
.
∴![]() ,
,![]() ,∵
,∵![]() ,
,
∴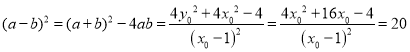 .
.
∴![]() ,解得
,解得![]() 或
或![]() (舍),∴
(舍),∴![]() .
.


科目:高中數學 來源: 題型:
【題目】以平面直角坐標系的原點![]() 為極點,
為極點,![]() 軸的正半軸為極軸,建立極坐標系,曲線
軸的正半軸為極軸,建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() ,將曲線
,將曲線![]() 繞極點逆時針旋轉
繞極點逆時針旋轉![]() 后得到曲線
后得到曲線![]() .
.
(Ⅰ)求曲線![]() 的極坐標方程;
的極坐標方程;
(Ⅱ)若直線![]() :
:![]() 與
與![]() ,
,![]() 分別相交于異于極點的
分別相交于異于極點的![]() ,
,![]() 兩點,求
兩點,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某地一條主于道上有46盞路燈,相鄰兩盞路燈之間間隔30米,有關部門想在所有相鄰路燈間都新添一盞,假設工人每次在兩盞燈之間添新路燈是隨機,并且每次添新路燈相互獨立.新添路燈與左右相鄰路燈的間隔都不小于10米是符合要求的,記符合要求的新添路燈數量為![]() ,則
,則![]() ( )
( )
A.30B.15C.10D.5
查看答案和解析>>
科目:高中數學 來源: 題型:
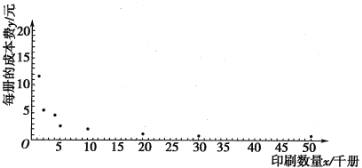
【題目】某公司為研究某種圖書每冊的成本費y(單位:元)與印刷數量x(單位:千冊)的關系,收集了一些數據并進行了初步處理,得到了下面的散點圖及一些統計量的值.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
表中![]() ,
,![]()
(1)根據散點圖判斷:![]() 與
與![]() 哪一個模型更適合作為該圖書每冊的成本費y與印刷數量x的回歸方程?(只要求給出判斷,不必說明理由)
哪一個模型更適合作為該圖書每冊的成本費y與印刷數量x的回歸方程?(只要求給出判斷,不必說明理由)
(2)根據(1)的判斷結果及表中數據,建立y關于x的回歸方程(結果精確到0.01);
(3)若該圖書每冊的定價為9.22元,則至少應該印刷多少冊才能使銷售利潤不低于80000元?(假設能夠全部售出,結果精確到1)
附:對于一組數據(ω1,v1),(ω2,v2),…,(ωn,vn),其回歸直線![]() 的斜率和截距的最小二乘估計分別為
的斜率和截距的最小二乘估計分別為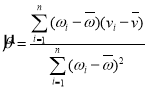 ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2020年春節期間,全國人民都在抗擊“新型冠狀病毒肺炎”的斗爭中.當時武漢多家醫院的醫用防護物資庫存不足,某醫院甚至面臨斷貨危機,南昌某生產商現有一批庫存的醫用防護物資,得知消息后,立即決定無償捐贈這批醫用防護物資,需要用A、B兩輛汽車把物資從南昌緊急運至武漢.已知從南昌到武漢有兩條合適路線選擇,且選擇兩條路線所用的時間互不影響.據調查統計2000輛汽車,通過這兩條路線從南昌到武漢所用時間的頻數分布表如下:
所用的時間(單位:小時) |
|
|
|
|
路線1的頻數 | 200 | 400 | 200 | 200 |
路線2的頻數 | 100 | 400 | 400 | 100 |
假設汽車A只能在約定交貨時間的前5小時出發,汽車B只能在約定交貨時間的前6小時出發(將頻率視為概率).為最大可能在約定時間送達這批物資,來確定這兩車的路線.
(1)汽車A和汽車B應如何選擇各自的路線.
(2)若路線1、路線2的“一次性費用”分別為3.2萬元、1.6萬元,且每車醫用物資生產成本為40萬元(其他費用忽略不計),以上費用均由生產商承擔,作為援助金額的一部分.根據這兩輛車到達時間分別計分,具體規則如下(已知兩輛車到達時間相互獨立,互不影響):
到達時間與約定時間的差x(單位:小時) |
|
|
|
該車得分 | 0 | 1 | 2 |
生產商準備根據運輸車得分情況給出現金排款,兩車得分和為0,捐款40萬元,兩車得分和每增加1分,捐款增加20萬元,若汽車A、B用(1)中所選的路線運輸物資,記該生產商在此次援助活動中援助總額為Y(萬元),求隨機變量Y的期望值,(援助總額![]() 一次性費用
一次性費用![]() 生產成本
生產成本![]() 現金捐款總額)
現金捐款總額)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com