【題目】在△ABC中， 
，O為平面內(nèi)一點，且 
，M為劣弧 
上一動點，且 
，
則p+q的最大值為 ．
【答案】2
【解析】解：∵ 
，
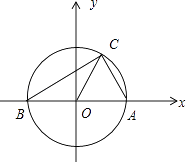
∴O是△ABC的外心．
∵∠A= 
，∴∠BOC= 
，
設(shè)OA=1，A（1，0），B（﹣1，0），C（ 
， 
），
則 
=p 
=（﹣p+ 
， 
），
設(shè)M（cosα，sinα），則 ≤α≤π，
∴ 
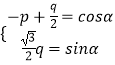，即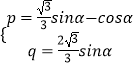 
，
∴p+q= 
sinα﹣cosα=2sin（α﹣ 
），
∵ ≤α≤π，∴ ≤ 
≤ 
，
∴當 = 
時，p+q取得最大值2．
故答案為：2．
本題考查的是由向量解決幾何問題，由數(shù)形結(jié)合法可得O是△ABC的外心．設(shè)OA=1，A（1，0），B（﹣1，0），C（ ， ）.設(shè)M（cosα，sinα），則 ≤α≤π，∴p+q= 3 sinα﹣cosα=2sin（α﹣ ），∵ ≤α≤π，∴ ≤ α ≤ . ∴當 α = 時，p+q取得最大值2
閱讀快車系列答案科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知點M（﹣1，0）和N（1，0），若某直線上存在點P，使得|PM|+|PN|=4，則稱該直線為“橢型直線”．現(xiàn)有下列直線：①x﹣2y+6=0；②x﹣y=0；③2x﹣y+1=0；④x+y﹣3=0．其中是“橢型直線”的是（ ）
A.①③
B.①②
C.②③
D.③④
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知a∈R，函數(shù)f（x）=2ln（x﹣2）﹣a（x﹣2）2
（Ⅰ）討論函數(shù)f（x）的單調(diào)性；
（Ⅱ）若函數(shù)f（x）有兩個相異零點x1 ， x2 ， 求證x1x2+4＞2（x1+x2）+e（其中e為自然對數(shù)的底數(shù)）
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知函數(shù)f（x）= 
，且f（2017）=2016，則f（﹣2017）=（ ）
A.﹣2014
B.﹣2015
C.﹣2016
D.﹣2017
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】以直角坐標系的原點O為極點，x軸正半軸為極軸，并在兩種坐標系中取相同的長度單位，已知直線l的參數(shù)方程為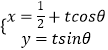 
，（t為參數(shù)，0＜θ＜π），曲線C的極坐標方程為ρsin2α﹣2cosα=0．
（1）求曲線C的直角坐標方程；
（2）設(shè)直線l與曲線C相交于A，B兩點，當θ變化時，求|AB|的最小值．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知函數(shù)f（x）=（x﹣2）ex﹣ 
x2 ， 其中a∈R，e為自然對數(shù)的底數(shù)
（Ⅰ）函數(shù)f（x）的圖象能否與x軸相切？若能與x軸相切，求實數(shù)a的值；否則，請說明理由；
（Ⅱ）若函數(shù)y=f（x）+2x在R上單調(diào)遞增，求實數(shù)a能取到的最大整數(shù)值．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】若函數(shù)f（x）= 
. （a＞0且a≠1），函數(shù)g（x）=f（x）﹣k．
①若a= 
，函數(shù)g（x）無零點，則實數(shù)k的取值范圍為；
②若f（x）有最小值，則實數(shù)a的取值范圍是 ．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】直線y=x+a與拋物線y2=5ax（a＞0）相交于A，B兩點，C（0，2a），給出下列4個命題：
p1：△ABC的重心在定直線7x﹣3y=0上，p2：|AB| 
的最大值為2 
；
p3：△ABC的重心在定直線 3x﹣7y=0上；p4：|AB| 的最大值為2 
．
其中的真命題為（ ）
A.p1 ， p2
B.p1 ， p4
C.p2 ， p3
D.p3 ， p4
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com