Question

【題目】已知函數．

（I）當時，求的單調區間和極值；

（II）若對于任意，都有成立，求k的取值范圍；

(Ⅲ)若，且，證明：．

Answer 1

【答案】（I）極小值為，無極大值；（II）；（3）見解析.

【解析】試題分析：（1）由題意x>0，由此根據k≤0，k>0利用導數性質分類討論，能求出函數f（x）的單調區間和極值．
（2）問題轉化為，對于x∈[e，e2]恒成立，令，則，令，由此利用導數性質能求出實數k的取值范圍．
（3）設，則，要證，只要證，即證，由此利用導數性質能證明.

試題解析：

（1），

①時，因為，所以，

函數的單調遞增區間是，無單調遞減區間，無極值；

②當時，令，解得，

當時，；當，．

所以函數的單調遞減區間是，單調遞增區間是，

在區間上的極小值為，無極大值．

（2）由題意，，

即問題轉化為對于恒成立，

即對于恒成立，

令，則，

令，則，

所以在區間上單調遞增，故，故，

所以在區間上單調遞增，函數．

要使對于恒成立，只要，

所以，即實數k的取值范圍為．

（3）證法1 因為，由（1）知，函數在區間上單調遞減，在區間上單調遞增，且．

不妨設，則，

要證，只要證，即證．

因為在區間上單調遞增，所以，

又，即證，

構造函數，

即，．

，

因為，所以，即，

所以函數在區間上單調遞增，故，

而，故，

所以，即，所以成立．

證法2 要證成立，只要證：.

因為，且，所以，

即，，

即，

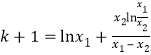，同理，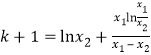

從而，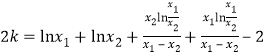

要證，只要證，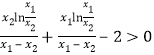

令不妨設，則，

即證，即證，

即證對恒成立，

設，，

所以在單調遞增，，得證，所以.