【題目】在銳角△ABC中，內角A，B，C的對邊分別為a，b，c，且2asinB= 
b．
（1）求角A的大小；
（2）若a=6，b+c=8，求△ABC的面積．
【答案】
（1）解：由2asinB= 
b，利用正弦定理得：2sinAsinB= sinB，
∵sinB≠0，∴sinA= 
，
又A為銳角，
則A= 
；
（2）解：由余弦定理得：a2=b2+c2﹣2bccosA，即36=b2+c2﹣bc=（b+c）2﹣3bc=64﹣3bc，
∴bc= 
，又sinA= ，
則S△ABC= 
bcsinA= 
【解析】（1）利用正弦定理化簡已知等式，求出sinA的值，由A為銳角，利用特殊角的三角函數值即可求出A的度數；（2）由余弦定理列出關系式，再利用完全平方公式變形，將a，b+c及cosA的值代入求出bc的值，再由sinA的值，利用三角形面積公式即可求出三角形ABC的面積．
閱讀快車系列答案科目：高中數學 來源： 題型：
【題目】已知
分別是橢圓
的長軸與短軸的一個端點， 
是橢圓的左、右焦點，以
點為圓心、3為半徑的圓與以
點為圓心、1為半徑的圓的交點在橢圓
上，且
．
（1）求橢圓
的方程；
（2）設
為橢圓
上一點，直線
與
軸交于點
，直線
與
軸交于點
，求證： 
．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）= 
，把函數g（x）=f（x）﹣x的零點按從小到大的順序排列成一個數列，則該數列的通項公式為（ ）
A.
B.an=n﹣1
C.an=n（n﹣1）
D.
查看答案和解析>>
科目：高中數學 來源： 題型：
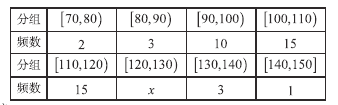
【題目】甲乙兩個學校高三年級分別有1100人，1000人，為了了解兩個學校全體高三年級學生在該地區二模考試的數學成績清況，采用分層抽樣方法從兩個學校一共抽取了105名學生的數學成績，并作出了頻數分布統計表如下：
甲校：
乙校:
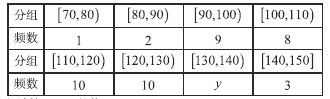
（1）計算
的值；
（2）若規定考試成績在
內為優秀，請根據樣本估計乙校數學成績的優秀率；
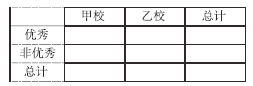
（3）由以上統計數據填寫下面
列聯表，并判斷是否有
的把握認為兩個學校的數學成績有差異.
附：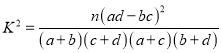 
； 
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在△ABC中，內角A，B，C的對邊分別為a，b，c，2cos（A﹣C）+cos2B=1+2cosAcosC．
（1）求證：a，b，c依次成等比數列；
（2）若b=2，求u=| 
|的最小值，并求u達到最小值時cosB的值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知向量 
=（cos 
x，sin x）， 
=（cos 
，﹣sin ），且x∈[﹣ 
， 
]
（1）求 及| + |；
（2）若f（x）= ﹣| + |，求f（x）的最大值和最小值．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
