
【題目】關于函數![]() 有下述四個結論:①若
有下述四個結論:①若![]() ,則
,則![]() ;②
;②![]() 的圖象關于點
的圖象關于點![]() 對稱;③函數
對稱;③函數![]() 在
在![]() 上單調遞增;④
上單調遞增;④![]() 的圖象向右平移
的圖象向右平移![]() 個單位長度后所得圖象關于
個單位長度后所得圖象關于![]() 軸對稱.其中所有正確結論的編號是( )
軸對稱.其中所有正確結論的編號是( )
A.①②④B.①②C.③④D.②④
科目:高中數學 來源: 題型:
【題目】(本題14分)下表提供了某廠節能降耗技術改造后生產甲產品過程中記錄的產量(![]() 噸)與相應的生產能耗
噸)與相應的生產能耗![]() (噸)標準煤的幾組對照數據:
(噸)標準煤的幾組對照數據:
| 3 | 4 | 5 | 6 |
| 2.5 | 3 | 4 | 4.5 |

(1)請畫出上表數據的散點圖;并指出x,y 是否線性相關;
(2)請根據上表提供的數據,用最小二乘法求出![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() ;
;
(3)已知該廠技術改造前100噸甲產品能耗為90噸標準煤,試根據(2)求出的線性回歸方程,預測生產100噸甲產品的生產能耗比技術改造前降低多少噸標準煤?
(參考:用最小二乘法求線性回歸方程系數公式 ,
,![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】過去大多數人采用儲蓄的方式將錢儲蓄起來,以保證自己生活的穩定![]() 考慮到通貨膨脹的壓力,如果我們把所有的錢都用來儲蓄,這并不是一種很好的方式
考慮到通貨膨脹的壓力,如果我們把所有的錢都用來儲蓄,這并不是一種很好的方式![]() 隨著金融業的發展,普通人能夠使用的投資理財工具也多了起來
隨著金融業的發展,普通人能夠使用的投資理財工具也多了起來![]() 為了研究某種理財工具的使用情況,現對
為了研究某種理財工具的使用情況,現對![]() 年齡段的人員進行了調查研究,將各年齡段人數分成5組:
年齡段的人員進行了調查研究,將各年齡段人數分成5組:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,并整理得到頻率分布直方圖:
,并整理得到頻率分布直方圖:
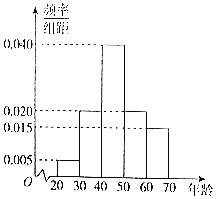
![]() Ⅰ
Ⅰ![]() 估計使用這種理財工具的人員年齡的中位數、平均數;
估計使用這種理財工具的人員年齡的中位數、平均數;
![]() Ⅱ
Ⅱ![]() 采用分層抽樣的方法,從第二組、第三組、第四組中共抽取8人,則三個組中各抽取多少人?
采用分層抽樣的方法,從第二組、第三組、第四組中共抽取8人,則三個組中各抽取多少人?
![]() Ⅲ
Ⅲ![]() 在
在![]() Ⅱ
Ⅱ![]() 中抽取的8人中,隨機抽取2人,則第三組至少有1個人被抽到的概率是多少?
中抽取的8人中,隨機抽取2人,則第三組至少有1個人被抽到的概率是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】古希臘著名數學家阿波羅尼斯與歐幾里得、阿基米德齊名.他發現:平面內到兩個定點![]() 的距離之比為定值
的距離之比為定值![]() 的點所形成的圖形是圓.后來,人們將這個圓以他的名字命名,稱為阿波羅尼斯圓,簡稱阿氏圓.已知在平面直角坐標系
的點所形成的圖形是圓.后來,人們將這個圓以他的名字命名,稱為阿波羅尼斯圓,簡稱阿氏圓.已知在平面直角坐標系![]() 中,
中,![]() ,
,![]() ,點
,點![]() 滿足
滿足![]() .設點
.設點![]() 所構成的曲線為
所構成的曲線為![]() ,下列結論正確的是( )
,下列結論正確的是( )
A.![]() 的方程為
的方程為![]()
B.在![]() 上存在點
上存在點![]() ,使得
,使得![]() 到點
到點![]() 的距離為
的距離為![]()
C.在![]() 上存在點
上存在點![]() ,使得
,使得![]()
D.在![]() 上存在點
上存在點![]() ,使得
,使得![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“倫敦眼”坐落在英國倫敦泰晤士河畔,是世界上首座觀景摩天輪,又稱“千禧之輪”,該摩天輪的半徑為6(單位:![]() ),游客在乘坐艙
),游客在乘坐艙![]() 升到上半空鳥瞰倫敦建筑
升到上半空鳥瞰倫敦建筑![]() ,倫敦眼與建筑之間的距離
,倫敦眼與建筑之間的距離![]() 為12(單位:
為12(單位:![]() ),游客在乘坐艙
),游客在乘坐艙![]() 看建筑
看建筑![]() 的視角為
的視角為![]() .
.

(1)當乘坐艙![]() 在倫敦眼的最高點
在倫敦眼的最高點![]() 時,視角
時,視角![]() ,求建筑
,求建筑![]() 的高度;
的高度;
(2)當游客在乘坐艙![]() 看建筑
看建筑![]() 的視角
的視角![]() 為
為![]() 時,拍攝效果最好.若在倫敦眼上可以拍攝到效果最好的照片,求建筑
時,拍攝效果最好.若在倫敦眼上可以拍攝到效果最好的照片,求建筑![]() 的最低高度.
的最低高度.
(說明:為了便于計算,數據與實際距離有誤差,倫敦眼的實際高度為![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() 中,角A,B,C的對邊為a,b,c,現給出以下四個命題:
中,角A,B,C的對邊為a,b,c,現給出以下四個命題:
![]() 當
當![]() ,
,![]() ,
,![]() 時,滿足條件的三角形共有1個;
時,滿足條件的三角形共有1個;
![]() 若三角形a:b:
若三角形a:b:![]() :5:7,這個三角形的最大角是
:5:7,這個三角形的最大角是![]() ;
;
![]() 如果
如果![]() ,那么
,那么![]() 的形狀是直角三角形;
的形狀是直角三角形;
![]() 若
若![]() ,
,![]() ,
,![]() ,則
,則![]() 在
在![]() 方向的投影為
方向的投影為![]() .
.
以上命題中所有正確命題的序號是______
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某商場親子游樂場由于經營管理不善突然倒閉.在進行資產清算時發現有3000名客戶辦理的充值會員卡上還有余額.為了了解客戶充值卡上的余額情況,從中抽取了300名客戶的充值卡余額進行統計.其中余額分組區間為![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,其頻率分布直方圖如圖所示,請你解答下列問題:
,其頻率分布直方圖如圖所示,請你解答下列問題:
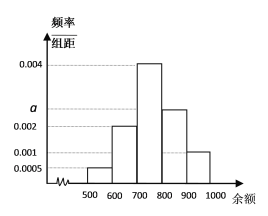
(1)求![]() 的值;
的值;
(2)求余額不低于![]() 元的客戶大約為多少人?
元的客戶大約為多少人?
(3)根據頻率分布直方圖,估計客戶人均損失多少?(用組中值代替各組數據的平均值).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() ,
,![]() 的線性回歸直線方程為
的線性回歸直線方程為![]() ,且
,且![]() ,
,![]() 之間的一組相關數據如下表所示,則下列說法錯誤的為
之間的一組相關數據如下表所示,則下列說法錯誤的為

A.變量![]() ,
,![]() 之間呈現正相關關系B.可以預測,當
之間呈現正相關關系B.可以預測,當![]() 時,
時,![]()
C.![]() D.由表格數據可知,該回歸直線必過點
D.由表格數據可知,該回歸直線必過點![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com