Question

【題目】如圖，多面體EF﹣ABCD中，ABCD是正方形，AC、BD相交于O，EF∥AC，點E在AC上的射影恰好是線段AO的中點．
（Ⅰ）求證：BD⊥平面ACF；
（Ⅱ）若直線AE與平面ABCD所成的角為60°，求平面DEF與平面ABCD所成角的正弦值．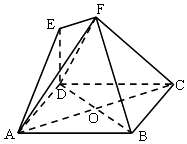

Answer 1

【答案】解：（Ⅰ）取AO的中點H，連結EH，則EH⊥平面ABCD
∵BD在平面ABCD內，∴EH⊥BD
又正方形ABCD中，AC⊥BD
∵EH∩AC=H，EH、AC在平面EACF內
∴BD⊥平面EACF，即BD⊥平面ACF
（Ⅱ）由（Ⅰ）知EH⊥平面ABCD，如圖，以H為原點， 分別為x軸，y軸，z軸的正方向建立空間直角坐標系H﹣xyz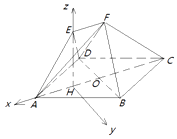

∵EH⊥平面ABCD，∴∠EAH為AE與平面ABCD所成的角，即∠EAH=60°，設正方形ABCD的邊長為4a，
則AC=4 ，AH= ，EA=2 ，EH=
各點坐標分別為H（0，0，0），A（ ，B（﹣
C（﹣3 ，D（﹣ ，E（0，0，
易知為平面ABCD的一個法向量，記 ，
， ，
∵EF∥AC，∴
設平面DEF的一個法向量為 ，則 ⊥ ， ⊥，
即 ，令z= ，則x=0，y=﹣2，∴ ，且 ，
∴ 與 的夾角θ為|cosθ|=
平面DEF與平面ABCD所成角α的正弦值為sinα=
【解析】（Ⅰ）取AO的中點H，連結EH，只需證EH⊥BD，AC⊥BD，即可得BD⊥平面ACF（Ⅱ）由（Ⅰ）知EH⊥平面ABCD，如圖，以H為原點， 分別為x軸，y軸，z軸的正方向建立空間直角坐標系H﹣xyz，求出兩個面的法向量，利用向量的夾角公式即可求解．
【考點精析】掌握直線與平面垂直的判定是解答本題的根本，需要知道一條直線與一個平面內的兩條相交直線都垂直，則該直線與此平面垂直；注意點：a)定理中的“兩條相交直線”這一條件不可忽視；b)定理體現了“直線與平面垂直”與“直線與直線垂直”互相轉化的數學思想．