【題目】某果農從經過篩選（每個水果的大小最小不低于50克，最大不超過100克）的10000個水果中抽取出100個樣本進行統計，得到如下頻率分布表：
級別 | 大小（克） | 頻數 | 頻率 |
一級果 |
| 5 | 0.05 |
二級果 |
|
| |
三級果 |
| 35 |
|
四級果 |
| 30 | |
五級果 |
| 20 | |
合計 | 100 |
請根據頻率分布表中所提供的數據，解得下列問題：
（1）求
的值，并完成頻率分布直方圖；
（2）若從四級果，五級果中按分層抽樣的方法抽取5個水果，并從中選出2個作為展品，求2個展品中僅有1個是四級果的概率；
（3）若將水果作分級銷售，預計銷售的價格
元/個與每個水果的大小
克關系是：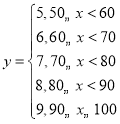
，則預計10000個水果可收入多少元？
【答案】（1）
的值為10，
的值為0.35；作圖見解析（2）
（3）
元
【解析】
（1）根據樣本總數為
可求，由頻數
樣本總數可求；計算出各組頻率，再計算出頻率/組距即可畫出頻率分布直方圖.
（2）根據分層抽樣可得抽取的4級有
個，抽取5級果有
個，設三個四級果分別記作：
，二個五級果分別記作：
，利用古典概型的概率計算公式即可求解.
（3）計算出100個水果的收入
即可預計10000個水果可收入.
（1）的值為10，的值為0.35
（2）四級果有30個，五級果有20個，按分層抽樣的方法抽取5個水果，
則抽取的4級果有
個，5級果有
個.
設三個四級果分別記作：，二個五級果分別記作：，
從
中任選二個作為展品的所有可能結果是
，
共有10種，
其中兩個展品中僅有一個是四級果的事件為
，
包含
共
個，
所求的概率為
.
（3）100個水果的收入為
（元）
所以10000個水果預計可收入
（元）.
課課通課程標準思維方法與能力訓練系列答案科目：高中數學 來源： 題型：
【題目】已知函數
，
.
（1）若函數
在區間
上的最大值和最小值之和為6，求實數
的值；
（2）設函數
，若函數
在區間
上恒有零點，求實數
的取值范圍；
（3）在問題（2）中，令
，比較
與0的大小關系，并說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，AOB是一塊半徑為r的扇形空地，
．某單位計劃在空地上修建一個矩形的活動場地OCDE及一矩形停車場EFGH，剩余的地方進行綠化．若
，設
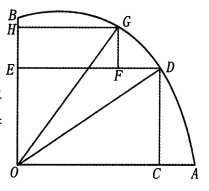
(Ⅰ)記活動場地與停車場占地總面積為
，求的表達式；
(Ⅱ)當
為何值時，可使活動場地與停車場占地總面積最大．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
： 
的左、右焦點分別為
和
，離心率是
，直線
過點
交橢圓于
， 
兩點，當直線
過點
時， 
的周長為
.
（Ⅰ）求橢圓
的標準方程；
（Ⅱ）當直線
繞點
運動時，試求
的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】一元線性同余方程組問題最早可見于中國南北朝時期（公元
世紀）的數學著作《孫子算經》卷下第二十六題，叫做“物不知數”問題，原文如下：有物不知數，三三數之剩二，五五數之剩三，問物幾何？即，一個整數除以三余二，除以五余三，求這個整數.設這個整數為
，當
時， 符合條件的共有_____個．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設
。
，
，
，
是
中的數所成的數列，它包含的不以1結尾的任何排列，即對于的四個數的任意一個不以1結尾的排列
，
，都有
，
，
，
，使得
，并且
，求這種數列的項數
的最小值。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
