【題目】如圖，在直四棱柱
中，
，
，
，
，
分別為
的中點，
（1）證明：
平面
.
（2）求直線
與平面
所成角的正弦值.
愉快的寒假南京出版社系列答案科目：高中數學 來源： 題型：
【題目】在平面直角坐標系xOy中，已知橢圓
的左、右焦點分別為F1，F2，點A在橢圓E上且在第一象限內，AF2⊥F1F2，直線AF1與橢圓E相交于另一點B．
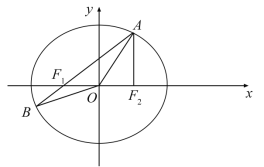
（1）求△AF1F2的周長；
（2）在x軸上任取一點P，直線AP與橢圓E的右準線相交于點Q，求
的最小值；
（3）設點M在橢圓E上，記△OAB與△MAB的面積分別為S1，S2，若S2=3S1，求點M的坐標．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某學校課外興趣小組利用假期到植物園開展社會實踐活動，研究某種植物生長情況與溫度的關系.現收集了該種植物月生長量y（cm）與月平均氣溫x（℃）的8組數據，并制成如圖所示的散點圖.
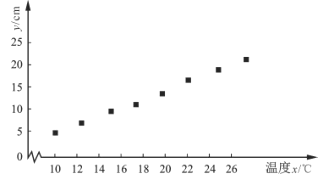
根據收集到的數據，計算得到如下值：
|
|
|
|
18 | 12.325 | 224.04 | 235.96 |
（1）求出y關于x的線性回歸方程（最終結果的系數精確到0.01），并求溫度為28℃時月生長量y的預報值；
（2）根據y關于x的回歸方程，得到殘差圖如圖所示，分析該回歸方程的擬合效果.
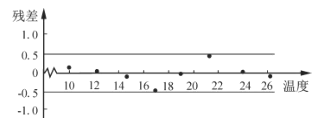
附：對于一組數據
，其回歸直線
的斜率和截距的最小二乘估計分別為
，
.
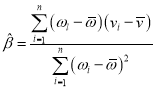查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】為滿足人民對美好生活的向往，環保部門要求相關企業加強污水治理，排放未達標的企業要限期整改，設企業的污水排放量W與時間t的關系為
，用
的大小評價在
這段時間內企業污水治理能力的強弱，已知整改期內，甲、乙兩企業的污水排放量與時間的關系如下圖所示.
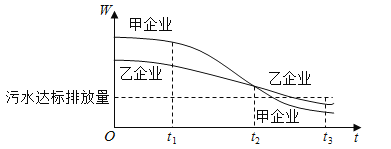
給出下列四個結論：
①在
這段時間內，甲企業的污水治理能力比乙企業強；
②在
時刻，甲企業的污水治理能力比乙企業強；
③在
時刻，甲、乙兩企業的污水排放都已達標；
④甲企業在
這三段時間中，在
的污水治理能力最強．
其中所有正確結論的序號是____________________．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某校高二年級進行選課走班，已知語文、數學、英語是必選學科，另外需從物理、化學、生物、政治、歷史、地理6門學科中任選3門進行學習. 現有甲、乙、丙三人，若同學甲必選物理，則下列結論正確的是（ ）
A.甲的不同的選法種數為10
B.甲、乙、丙三人至少一人選化學與全選化學是對立事件
C.乙同學在選物理的條件下選化學的概率是
D.乙、丙兩名同學都選物理的概率是
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在①
，②
，③
這三個條件中選擇兩個，補充在下面問題中，并給出解答.已知數列
的前
項和為
，滿足________，________；又知正項等差數列
滿足
，且
，
，
成等比數列.
（1）求和的通項公式；
（2）證明：
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某工廠的某種產品成箱包裝，每箱200件，每一箱產品在交付用戶之前要對產品作檢驗，如檢驗出不合格品，則更換為合格品．檢驗時，先從這箱產品中任取20件作檢驗，再根據檢驗結果決定是否對余下的所有產品作檢驗，設每件產品為不合格品的概率都為
，且各件產品是否為不合格品相互獨立．
（1）記20件產品中恰有2件不合格品的概率為
,求的最大值點
．
（2）現對一箱產品檢驗了20件，結果恰有2件不合格品，以（1）中確定的作為
的值．已知每件產品的檢驗費用為2元，若有不合格品進入用戶手中，則工廠要對每件不合格品支付25元的賠償費用．
（i）若不對該箱余下的產品作檢驗，這一箱產品的檢驗費用與賠償費用的和記為
，求
;
（ii）以檢驗費用與賠償費用和的期望值為決策依據，是否該對這箱余下的所有產品作檢驗？
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
