
【題目】已知函數f(x)=mx-lnx-1(m為常數).
(1)若函數f(x)恰有1個零點,求實數m的取值范圍;
(2)若不等式mx-ex≤f(x)+a對正數x恒成立,求實數a的最小整數值.
【答案】(1){m|m≤0或m=1}(2)實數a的最小整數值為-1
【解析】
(1)首先寫出f(x)的定義域,函數f(x)恰有1個零點方程f(x)=0僅有一個正實數解,由f(x)=0,得![]() ,設g(x)
,設g(x)![]() ,然后求導,找出g(x)的最值,結合圖象求出m的范圍;
,然后求導,找出g(x)的最值,結合圖象求出m的范圍;
(2)mx-ex≤f(x)+alnx-ex≤a-1.設h(x)=lnx-ex,求導判斷h(x)的單調區間,利用單調性求出a的最值即可.
解:(1)f(x)的定義域為(0,+∞),
函數f(x)恰有1個零點方程f(x)=0僅有一個正實數解,
由f(x)=0,得![]() ,
,
設g(x)![]() ,則
,則![]() ,
,
令g′(x)>0.得0<x<1,
令g′(x)<0,得x>1,
∴g(x)在(0,1)上單調遞增,在(1,+∞)上單調遞減,
∴g(x)在x=1處取得唯一的極大值,即為最大值,
故g(x)的最大值為g(1)=1.
當x趨近于0時,lnx+1趨近于-∞,
所以g(x)為負數,
當x趨近于+∞時,x的增長速度大于lnx+1的增長速度,
且當x>1時![]() ,
,
故g(x)趨近于0,
由圖可知,當m≤0或者m=1時,方程m=g(x)僅有一個實數解,
∴m的取值范圍為{m|m≤0或m=1};
(2)∵mx-ex≤f(x)+a,
∴lnx-ex≤a-1,
設h(x)=lnx-ex,
∴![]()
又∵![]() 在(0,+∞)上為減函數,h′(1)=1-e<0,
在(0,+∞)上為減函數,h′(1)=1-e<0,![]() ,
,
∴![]() 存在唯一的零點
存在唯一的零點![]() ,
,
此時h(x)在(0,x0)上單調遞增,在(x0,+∞)上單調遞減,/p>
且![]() =0,
=0,
∴![]() ,x0=-lnx0,
,x0=-lnx0,
由單調性知![]() =-(x0+
=-(x0+![]() ),
),
又![]() ,故
,故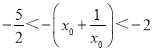 ,
,
∴mx-ex≤f(x)+a對任意正數x恒成立時,a-1≥-2,
∴a≥-1,
∴實數a的最小整數值為-1.


 一本好題口算題卡系列答案
一本好題口算題卡系列答案科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為![]() ,(
,( ![]() 為參數),
為參數),![]() 為曲線
為曲線![]() 上的動點,動點
上的動點,動點![]() 滿足
滿足![]() (
(![]() 且
且![]() ),
),![]() 點的軌跡為曲線
點的軌跡為曲線![]() .
.
(1)求曲線![]() 的方程,并說明
的方程,并說明![]() 是什么曲線;
是什么曲線;
(2)在以坐標原點為極點,以![]() 軸的正半軸為極軸的極坐標系中,
軸的正半軸為極軸的極坐標系中, ![]() 點的極坐標為
點的極坐標為![]() ,射線
,射線![]() 與
與![]() 的異于極點的交點為
的異于極點的交點為![]() ,已知
,已知![]() 面積的最大值為
面積的最大值為![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系xOy中,已知直線l過點P(2,2).以坐標原點為極點,x軸正半軸為極軸建立極坐標系,曲線C的極坐標方程為ρ﹣ρcos2θ﹣4cosθ=0.
(1)求C的直角坐標方程;
(2)若l與C交于A,B兩點,求 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
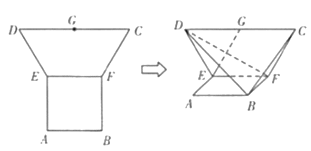
【題目】在平面多邊形![]() 中,四邊形
中,四邊形![]() 是邊長為2的正方形,四邊形
是邊長為2的正方形,四邊形![]() 為等腰梯形,
為等腰梯形,![]() 為
為![]() 的中點,
的中點,![]() ,現將梯形
,現將梯形![]() 沿
沿![]() 折疊,使平面
折疊,使平面![]() 平面
平面![]() .
.
(1)求證:![]() 面
面![]() ;
;
(2)求![]() 與平面
與平面![]() 成角的正弦值.
成角的正弦值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com