【題目】某出租車公司響應國家節能減排的號召，已陸續購買了140輛純電動汽車作為運營車輛，目前我國主流純電動汽車按續航里程數
．（單位：公里）分為3類，即
類：
，
類：
， 
類：
，該公司對這140輛車的行駛總里程進行統計，結果如下表：
類型 |
|
|
|
已行駛總里程不超過10萬公里的車輛數 | 10 | 40 | 30 |
已行駛總里程超過10萬公里的車輛數 | 20 | 20 | 20 |
（1）從這140輛汽車中任取一輛，求該車行駛總里程超過10萬公里的概率；
（2）公司為了了解這些車的工作狀況，決定抽取了14輛車進行車況分析，按表中描述的六種情況進行分層抽樣，設從
類車中抽取了
輛車．
①求
的值；
②如果從這
輛車中隨機選取兩輛車，求恰有一輛車行駛總里程超過10萬公里的概率．
【答案】（1）
；（2）①
；②
.
【解析】
試題分析：（1）由表可得總里程超出
萬公里的車輛數,再求概率；（2）由按比例的分層抽樣可得
的值,可列出從
輛車中隨機選取兩輛佃的所有情況,再找出恰有一車行駛總里程超過
萬公里的情況,利用古典概型可得結果.
試題解析：
（1）從這140輛汽車中任取一輛，則該車行駛總里程超過10萬公里的概率為
．
（2）①依題意
．
②5輛車中已行駛總里程不超過10萬公里的車有3輛，記為
；5輛車中已行駛總里程超過10萬公里的車有2輛，記為
．
“從5輛車中隨機選取兩輛車”的所有選法共10種：
．
“從5輛車中隨機選取兩輛車，恰有一輛車行駛里程超過10萬公里“的選法共6種：
．
則選取兩輛車中恰有一輛車行駛里程超過10萬公里的概率
．
新課標同步訓練系列答案
一線名師口算應用題天天練一本全系列答案科目：高中數學 來源： 題型：
【題目】已知函數f（x）=Asin（wx+φ）（x∈R，w＞0，0＜φ＜ 
）的部分圖象如圖所示．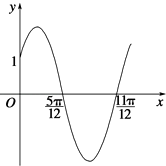 
（1）求函數f（x）的解析式；
（2）求函數g（x）=f（x﹣ 
）﹣f（x+ ）的單調遞增區間．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知數列{an}的前n項和Sn=3n+m（m為常數，n∈N+）
（1）求a1 ， a2 ， a3；
（2）若數列{an}為等比數列，求常數m的值及an；
（3）對于（2）中的an ， 記f（n）=λa2n+1﹣4λan+1﹣7，若f（n）＜0對任意的正整數n恒成立，求實數λ的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖所示，在四棱錐
中， 
平面
是
的中點， 
是
上的點且
為
邊
上的高.
（1）證明： 
平面
；
（2）若
，求三棱錐
的體積；
（3）在線段
上是否存在這樣一點
，使得
平面
?若存在，說出
點的位置.
查看答案和解析>>
科目：高中數學 來源： 題型：
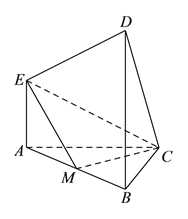
【題目】在如圖所示的多面體中， 
平面
， 
平面
， 
，且
， 
是
的中點．
（Ⅰ）求證： 
．
（Ⅱ）求平面
與平面
所成的銳二面角的余弦值．
（Ⅲ）在棱
上是否存在一點
，使得直線
與平面
所成的角是
．若存在，指出點
的位置；若不存在，請說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】選修4-4：坐標系與參數方程
在平面直角坐標系
中，以坐標原點
為極點， 
軸正半軸為極軸建立極坐標系，已知曲線
的極坐標方程為： 
，直線
的參數方程是
（
為參數， 
）．
（1）求曲線
的直角坐標方程；
（2）設直線
與曲線
交于兩點
，且線段
的中點為
，求
．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
