
【題目】已知![]() .
.
(1)當![]() 時,
時,![]() 的值域是
的值域是![]() ,試求實數
,試求實數![]() 的值;
的值;
(2)設關于![]() 的方程
的方程![]() 的兩個實根為
的兩個實根為![]() ;試問:是否存在實數
;試問:是否存在實數![]() ,使得不等式
,使得不等式![]() 對任意
對任意![]() 及
及![]() 恒成立?若存在,求實數
恒成立?若存在,求實數![]() 的取值范圍;若不存在,請說明理由.
的取值范圍;若不存在,請說明理由.
【答案】(1)![]() ;(2)存在,
;(2)存在,![]() 或
或![]() .
.
【解析】
(1)通過求導,判斷函數![]() 的單調區間,再由函數最小值列出方程解出
的單調區間,再由函數最小值列出方程解出![]() 的值;(2)化簡
的值;(2)化簡![]() ,利用韋達定理求出
,利用韋達定理求出![]() ,則問題等價于:是否存在實數
,則問題等價于:是否存在實數![]() ,使得不等式
,使得不等式![]() 對任意
對任意![]() 及
及![]() 恒成立,設
恒成立,設![]()
![]() ,根據
,根據![]() 的范圍可得
的范圍可得![]() 的最大值,代入不等式,將其看作關于
的最大值,代入不等式,將其看作關于![]() 的一次函數,再討論求出
的一次函數,再討論求出![]() 的取值范圍即得.
的取值范圍即得.
(1)由題![]() ,
,![]() ,
,
當![]() 時,函數
時,函數![]() 在區間
在區間![]() 是單調遞增,故
是單調遞增,故![]() ,解得:
,解得:![]() .
.
當![]() 時,
時,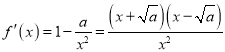 ,
,![]() 在區間
在區間![]() 單調遞減,在
單調遞減,在![]() 單調遞增,
單調遞增,
則![]() 在
在![]() 處取得最小值,故
處取得最小值,故![]() ,
,![]() ,無解.
,無解.
綜上,![]() .
.
(2)由題得,![]() ,化簡整理得
,化簡整理得![]() .
.
![]() ,
,![]() 方程
方程![]() 有兩個非零實根
有兩個非零實根![]() ,
,
可得![]() ,則有
,則有![]() =
=![]() =
=![]() ,
,
本題等價于是否存在![]() ,使不等式
,使不等式
![]()
![]() ——①
——①
對任意![]() ,
,![]() 恒成立.
恒成立.
把![]() 看作關于
看作關于![]() 的函數
的函數![]()
![]() ,則①式等價于
,則①式等價于
![]()
![]() ——②
——②
![]() ,
,![]()
![]()
![]() ,從而②式轉化為
,從而②式轉化為
![]() 3,
3,
即![]() ——③
——③
對![]() 恒成立,
恒成立,
把③式的左邊看作![]() 的函數,記
的函數,記![]()
![]() =
=![]() ,
,
若![]() ,③式顯然不成立;
,③式顯然不成立;
若![]() ,
,![]() 是
是![]() 的一次函數,要使
的一次函數,要使![]() 對
對![]() 恒成立,只要
恒成立,只要![]() 和
和![]() 同時成立即可,解不等式組
同時成立即可,解不等式組
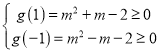 ,
,
得![]() 或
或![]() .
.
故存在實數![]() ,使不等式
,使不等式![]()
![]() 對任意
對任意![]() ,
,![]() 恒成立,其取值范圍是
恒成立,其取值范圍是![]() 或
或![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】設全集U=R,集合A={x|1≤x<4},B={x|2a≤x<3-a}.
(1)若a=-2,求B∩A,B∩(UA);(2)若A∪B=A,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知集合A={x|2a+1≤x≤3a-5},B={x|x<-1,或x>16},分別根據下列條件求實數a的取值范圍.
(1)A∩B=![]() ;(2)A(A∩B).
;(2)A(A∩B).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】用清水漂洗衣服上殘留的洗衣液,對用一定量的清水漂洗一次的效果作如下假定:用1個單位量的水可洗掉衣服上殘留洗衣液質量的一般,用水越多漂洗效果越好,但總還有洗衣液殘留在衣服上.設用![]() 單位量的清水漂洗一次后,衣服上殘留的洗衣液質量與本次漂洗前殘留的洗衣液質量之比為函數
單位量的清水漂洗一次后,衣服上殘留的洗衣液質量與本次漂洗前殘留的洗衣液質量之比為函數![]() ,其中
,其中![]() .
.
(1)試規定![]() 的值,并解釋其實際意義;
的值,并解釋其實際意義;
(2)根據假定寫出函數![]() 應該滿足的條件和具有的性質,并寫出滿足假定的一個指數函數;
應該滿足的條件和具有的性質,并寫出滿足假定的一個指數函數;
(3)設函數![]() .現有
.現有![]() (
(![]() )單位量的清水,可供漂洗一次,也可以把水平均分成2份后先后漂洗兩次,試確定哪種方式漂洗效果更好?并說明理由.
)單位量的清水,可供漂洗一次,也可以把水平均分成2份后先后漂洗兩次,試確定哪種方式漂洗效果更好?并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
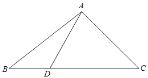
【題目】如圖所示,在△ABC中,D是BC邊上的一點,且AB=14,BD=6,∠ADC=![]() ,
,![]() .
.
(Ⅰ)求sin∠DAC;
(Ⅱ)求AD的長和△ABC的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓C的圓心在直線![]() 上,且圓C與x軸交于兩點
上,且圓C與x軸交于兩點![]() ,
,![]() .
.
(1)求圓C的方程;
(2)已知圓M:![]() ,設
,設![]() 為坐標平面上一點,且滿足:存在過點
為坐標平面上一點,且滿足:存在過點![]() 且互相垂直的直線
且互相垂直的直線![]() 和
和![]() 有無數對,它們分別與圓C和圓M相交,且圓心C到直線
有無數對,它們分別與圓C和圓M相交,且圓心C到直線![]() 的距離是圓心M到直線
的距離是圓心M到直線![]() 的距離的2倍,試求所有滿足條件的點
的距離的2倍,試求所有滿足條件的點![]() 的坐標
的坐標
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 對一切實數
對一切實數![]() ,
,![]() 都有
都有![]() 成立,且
成立,且![]() .
.
(1)求![]() 的值;
的值;
(2)求![]() 的解析式;
的解析式;
(3)已知![]() ,設
,設![]() :當
:當![]() 時,不等式
時,不等式![]() 恒成立;
恒成立;![]() :當
:當![]() 時,
時,![]() 是單調函數.如果滿足
是單調函數.如果滿足![]() 成立的
成立的![]() 的集合記為
的集合記為![]() ,滿足
,滿足![]() 成立的
成立的![]() 的集合記為
的集合記為![]() ,求
,求![]() (
(![]() 為全集).
為全集).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com