【題目】汽車“定速巡航”技術是用于控制汽車的定速行駛，當汽車被設定為定速巡航狀態時，電腦根據道路狀況和汽車的行駛阻力自動控制供油量，使汽車始終保持在所設定的車速行駛，而無需司機操縱油門，從而減輕疲勞，促進安全，節省燃料.某汽車公司為測量某型號汽車定速巡航狀態下的油耗情況，選擇一段長度為240km的平坦高速路段進行測試.經多次測試得到一輛汽車每小時耗油量F（單位：L）與速度v（單位：km/h）（
）的下列數據：
v | 0 | 40 | 60 | 80 | 120 |
F | 0 |
|
| 10 | 20 |
為了描述汽車每小時耗油量與速度的關系，現有以下三種函數模型供選擇：
，
，
.
（1）請選出你認為最符合實際的函數模型，并求出相應的函數解析式.
（2）這輛車在該測試路段上以什么速度行駛才能使總耗油量最少？
【答案】（1）選擇函數
,
（2）這輛車在該測試路段上以80km/h的速度行駛時總耗油量最少
【解析】
（1）根據表中數據分析可知，所選模型必須滿足定義域為
，且在上為增函數，故選，在代入數據計算可得.
（2）設這輛車在該測試路段的總耗油量為y，行駛時間為t，由題意得：
，根據二次函數的性質求出最值.
解：（1）由題意可知，符合本題的函數模型必須滿足定義域為，且在上為增函數；
函數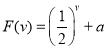
在是減函數，所以不符合題意；
而函數
的
，即定義域不可能為，也不符合題意；
所以選擇函數.
由已知數據得：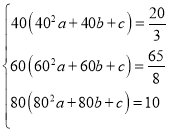
解得：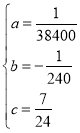
所以，
（2）設這輛車在該測試路段的總耗油量為y，行駛時間為t，由題意得：
因為
，所以，當
時，y有最小值30.
所以，這輛車在該測試路段上以80km/h的速度行駛時總耗油量最少，最少為30L.
快捷英語周周練系列答案科目：高中數學 來源： 題型：
【題目】漢代數學家趙爽在注解《周髀算經》時給出的“趙爽弦圖”（如下圖），四個全等的直角三角形（朱實），可以圍成一個大的正方形，中空部分為一個小正方形（黃實）．若直角三角形中一條較長的直角邊為8，直角三角形的面積為24，若在上面扔一顆玻璃小球，則小球落在“黃實”區域的概率為（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，矩形
中，
，
為邊
的中點，將
沿直線
翻折成
．若
為線段
的中點，則在翻折過程中，下面四個命題中不正確的是（ ）
A. 
是定值
B. 點在某個球面上運動
C. 存在某個位置，使
D. 存在某個位置，使
平面
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】（題文）如圖所示的某種容器的體積為
，它是由圓錐和圓柱兩部分連接而成，圓柱與圓錐的底面半徑都為
．圓錐的高為
，母線與底面所成的角為
；圓柱的高為
，已知圓柱底面的造價為
元
，圓柱側面造價為
元，圓錐側面造價為
元．
（1）將圓柱的高
表示為底面半徑
的函數，并求出定義域；
（2）當容器造價最低時，圓柱的底面半徑為多少？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某公司一年需購買某種原料400噸，設公司每次都購買
噸，每次運費為4萬元，一年的總存儲費用為
萬元.
（1）要使一年的總運費與總存儲費用之和最小，則每次購買多少噸？
（2）要使一年的總運費與總存儲費用之和不超過200萬元，則每次購買量在什么范圍？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某學校為了制定治理學校門口上學、放學期間家長接送孩子亂停車現象的措施，對全校學生家長進行了問卷調查.根據從中隨機抽取的50份調查問卷，得到了如下的列聯表：
同意限定區域停車 | 不同意限定區域停車 | 合計 | |
男 | 20 | 5 | 25 |
女 | 10 | 15 | 25 |
合計 | 30 | 20 | 50 |
則認為“是否同意限定區域停產與家長的性別有關”的把握約為__________．
附：
，其中
.
| 0.050 | 0.005 | 0.001 |
| 3.841 | 7.879 | 10.828 |
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知曲線 y = x3 + x－2 在點 P0 處的切線
平行于直線
4x－y－1=0，且點 P0 在第三象限,
⑴求P0的坐標;
⑵若直線
, 且 l 也過切點P0 ,求直線l的方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
