【題目】某加工廠需定期購買原材料，已知每公斤原材料的價格為1.5元，每次購買原材料需支付運費600元，每公斤原材料每天的保管費用為0.03元，該廠每天需要消耗原材料400公斤，每次購買的原材料當天即開始使用（即有400公斤不需要保管）.
（Ⅰ）設該廠每x天購買一次原材料，試寫出每次購買的原材料在x天內總的保管費用y1關于x的函數關系式；
（Ⅱ）求該廠多少天購買一次原材料才能使平均每天支付的總費用y最少，并求出這個最少（小）值；
【答案】（Ⅰ）y=6x2－6x（x∈N*，x>1) （Ⅱ）當10天購買一次，最少費用為714元.
【解析】
試題分析：（1）由題知每次購買的原材料在x天內總的保管費用y1=每公斤每天的保管費用×每天需要消耗原材料×使用的天數可得函數關系式；（2）由（1）表示出購買一次原材料的總的費用，利用基本不等式求出y的最小值及此時的x的值即可
試題解析：（1）∵第一天的保管費a1=(400x－400)×0.03=12x－12；
第二天的保管費a2=12x－24，……，組成一個公差為－12的等差數列，
其中項數為：x－1項，（x∈N*，x>1).
∴y1=(x－1)×12(x－1)+
=6x2－6x（x∈N*，x>1)
（2）y=
·(y1+600+400x·1.5)=6x+
+594≥120+594=714(元).
當且僅當6x=，即x=10(天)時取“=”號，
∴當10天購買一次，最少費用為714元.
科目：高中數學 來源： 題型：
【題目】已知兩直線l1：ax﹣by+4=0，l2：（a﹣1）x+y+b=0，分別求滿足下列條件的a，b值
（1）l1⊥l2，且直線l1過點（﹣3，﹣1）；
（2）l1∥l2，且直線l1在兩坐標軸上的截距相等．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，已知長方形
中，
為
的中點，將
沿
折起，使得平面
平面
．
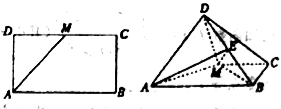
（1）求證：
；
（2）若點
是線段
上的一動點，問點
在何位置時，三棱錐
的體積與四棱錐
的體積之比為1：3？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】給出下列四個命題中：
①函數
的一個對稱中心為
；
②若
， 
為第一象限角，且
，則
；
③若
，則存在實數
，使得
；
④點
是三角形
所在平面內一點，且滿足
，則點
是三角形
的內心.
其中正確的序號是__________．（把你認為正確的序號都填上）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在某次測驗中，有6位同學的平均成績為75分， 用xn表示編號為n（n＝1，2，…，6）的同學所得成績，且前5位同學的成績如下：
編號n | 1 | 2 | 3 | 4 | 5 |
成績xn | 70 | 76 | 72 | 70 | 72 |
（1）求第6位同學的成績x6，及這6位同學成績的標準差s；
（2）從前5位同學中選2位同學，求恰有1位同學成績在區間（68，75）中的概率．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在直角坐標系
中，以原點
為極點，以
軸的正半軸為極軸建立極坐標系，已知曲線
的極坐標方程為
．
（1）求曲線
的直角坐標方程并指出其形狀；
（2）設
是曲線
上的動點，求
的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設數列{an}的前n項和為Sn，且首項a1≠3，an＋1＝Sn＋3n（n∈N*）．
（1）求證：數列{Sn－3n}是等比數列；
（2）若{an}為遞增數列，求a1的取值范圍．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
