
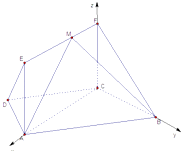
【題目】如圖,在梯形ABCD中,AB∥CD,AD=DC=CB=1,∠ABC=60°,四邊形ACFE為矩形,平面ACFE⊥平面ABCD,CF=1.
(Ⅰ)求證:BC⊥平面ACFE;
(Ⅱ)點M在線段EF上運動,設平面MAB與平面FCB所成二面角的平面角為θ(θ≤90°),試求cosθ的取值范圍.
【答案】解:(I)證明:在梯形ABCD中,
∵AB∥CD,AD=DC=CB=1,∠ABC=60°,
∴AB=2
∴AC2=AB2+BC2﹣2ABBCcos60°=3
∴AB2=AC2+BC2
∴BC⊥AC
∵平面ACFE⊥平面ABCD,平面ACFE∩平面ABCD=AC,BC平面ABCD
∴BC⊥平面ACFE
(II)由(I)可建立分別以直線CA,CB,CF為x軸,y軸,z軸的如圖所示空間直角坐標系,
令 ![]() ,則
,則 ![]() ,B(0,1,0),M(λ,0,1)
,B(0,1,0),M(λ,0,1)
∴ ![]()
設 ![]() 為平面MAB的一個法向量,
為平面MAB的一個法向量,
由 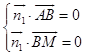 得
得 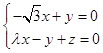
取x=1,則 ![]() ,
,
∵ ![]() 是平面FCB的一個法向量
是平面FCB的一個法向量
∴ 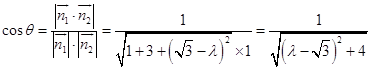
∵ ![]() ∴當λ=0時,cosθ有最小值
∴當λ=0時,cosθ有最小值 ![]() ,
,
當 ![]() 時,cosθ有最大值
時,cosθ有最大值 ![]() .
.
∴ 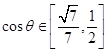 .
.
【解析】(I)證明線面垂直可以利用面面垂直進行證明,即若兩個平面垂直并且其中一個平面內的一條直線a與兩個平面的交線操作時則直線a與另一個平面垂直,即可證明線面垂直.(II)建立空間坐標系,根據坐標表示出兩個平面的法向量,結合向量的有關運算求出二面角的余弦的表達式,再利用函數的有關知識求出余弦的范圍.
【考點精析】解答此題的關鍵在于理解直線與平面垂直的判定的相關知識,掌握一條直線與一個平面內的兩條相交直線都垂直,則該直線與此平面垂直;注意點:a)定理中的“兩條相交直線”這一條件不可忽視;b)定理體現了“直線與平面垂直”與“直線與直線垂直”互相轉化的數學思想.


科目:高中數學 來源: 題型:
【題目】東莞市公交公司為了方便廣大市民出行,科學規劃公交車輛的投放,計劃在某個人員密集流動地段增設一個起點站,為了研究車輛發車的間隔時間![]() 與乘客等候人數
與乘客等候人數![]() 之間的關系,選取一天中的六個不同的時段進行抽樣調查,經過統計得到如下數據:
之間的關系,選取一天中的六個不同的時段進行抽樣調查,經過統計得到如下數據:
間隔時間( | 8 | 10 | 12 | 14 | 16 | 18 |
等候人數( | 16 | 19 | 23 | 26 | 29 | 33 |
調查小組先從這6組數據中選取其中的4組數據求得線性回歸方程,再用剩下的2組數據進行檢驗,檢驗方法如下:先用求得的線性回歸方程計算間隔時間對應的等候人數![]() ,再求
,再求![]() 與實際等候人數
與實際等候人數![]() 的差,若兩組差值的絕對值均不超過1,則稱所求的回歸方程是“理想回歸方程”.
的差,若兩組差值的絕對值均不超過1,則稱所求的回歸方程是“理想回歸方程”.
參考公式:用最小二乘法求線性回歸方程![]() 的系數公式:
的系數公式: ,
,
(1)若選取的是前4組數據,求![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() ;
;
(2)判斷(1)中的方程是否是“理想回歸方程”:
(3)為了使等候的乘客不超過38人,試用(1)中方程估計間隔時間最多可以設置為多少分鐘?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某地隨著經濟的發展,居民收入逐年增長,如表是該地一建設銀行連續五年的儲蓄存款(年底余額),如表1
年份x | 2011 | 2012 | 2013 | 2014 | 2015 |
儲蓄存款y(千億元) | 5 | 6 | 7 | 8 | 10 |
為了研究計算的方便,工作人員將上表的數據進行了處理,![]() 得到表2:
得到表2:
時間代號t | 1 | 2 | 3 | 4 | 5 |
z | 0 | 1 | 2 | 3 | 5 |
(1)求z關于t的線性回歸方程;
(2)通過(1)中的方程,求出y關于x的回歸方程;
(3)用所求回歸方程預測到2010年年底,該地儲蓄存款額可達多少?
附:對于線性回歸方程![]() ,
,
其中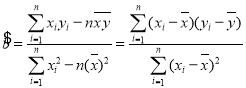 ,
, ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知定義在(0,+∞)上的連續函數y=f(x)滿足:xf′(x)﹣f(x)=xex且f(1)=﹣3,f(2)=0.則函數y=f(x)( )
A.有極小值,無極大值
B.有極大值,無極小值
C.既有極小值又有極大值
D.既無極小值又無極大值
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,在正方體![]() 中,側面對角線
中,側面對角線![]() ,
,![]() 上分別有一點E,F,且
上分別有一點E,F,且![]() ,則直線EF與平面ABCD所成的角的大小為( )
,則直線EF與平面ABCD所成的角的大小為( )

A.0°B.60°C.45°D.30°
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某書店剛剛上市了《中國古代數學史》,銷售前該書店擬定了5種單價進行試銷,每種單價(![]() 元)試銷l天,得到如表單價
元)試銷l天,得到如表單價![]() (元)與銷量
(元)與銷量![]() (冊)數據:
(冊)數據:
單價 | 18 | 19 | 20 | 21 | 22 |
銷量 | 61 | 56 | 50 | 48 | 45 |
(l)根據表中數據,請建立![]() 關于
關于![]() 的回歸直線方程:
的回歸直線方程:
(2)預計今后的銷售中,銷量![]() (冊)與單價
(冊)與單價![]() (元)服從(l)中的回歸方程,已知每冊書的成本是12元,書店為了獲得最大利潤,該冊書的單價應定為多少元?
(元)服從(l)中的回歸方程,已知每冊書的成本是12元,書店為了獲得最大利潤,該冊書的單價應定為多少元?
附: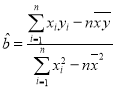 ,
,![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若一個人下半身長(肚臍至足底)與全身長的比近似為![]() (
(![]() ,稱為黃金分割比),堪稱“身材完美”,且比值越接近黃金分割比,身材看起來越好,若某人著裝前測得頭頂至肚臍長度為72
,稱為黃金分割比),堪稱“身材完美”,且比值越接近黃金分割比,身材看起來越好,若某人著裝前測得頭頂至肚臍長度為72![]() ,肚臍至足底長度為103
,肚臍至足底長度為103![]() ,根據以上數據,作為形象設計師的你,對TA的著裝建議是( )
,根據以上數據,作為形象設計師的你,對TA的著裝建議是( )
A.身材完美,無需改善B.可以戴一頂合適高度的帽子
C.可以穿一雙合適高度的增高鞋D.同時穿戴同樣高度的增高鞋與帽子
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設甲、乙、丙三個乒乓球協會分別選派3,1,2名運動員參加某次比賽,甲協會運動員編號分別為![]() ,
,![]() ,
,![]() ,乙協會編號為
,乙協會編號為![]() ,丙協會編號分別為
,丙協會編號分別為![]() ,
,![]() ,若從這6名運動員中隨機抽取2名參加雙打比賽.
,若從這6名運動員中隨機抽取2名參加雙打比賽.
(1)用所給編號列出所有可能抽取的結果;
(2)求丙協會至少有一名運動員參加雙打比賽的概率;
(3)求參加雙打比賽的兩名運動員來自同一協會的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com