
【題目】已知橢圓![]() ,圓心為坐標(biāo)原點的單位圓O在C的內(nèi)部,且與C有且僅有兩個公共點,直線
,圓心為坐標(biāo)原點的單位圓O在C的內(nèi)部,且與C有且僅有兩個公共點,直線![]() 與C只有一個公共點.
與C只有一個公共點.
(1)求C的標(biāo)準(zhǔn)方程;
(2)設(shè)不垂直于坐標(biāo)軸的動直線l過橢圓C的左焦點F,直線l與C交于A,B兩點,且弦AB的中垂線交x軸于點P,試求![]() 的面積的最大值.
的面積的最大值.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)根據(jù)單位圓O在C的內(nèi)部,且與C有且僅有兩個公共點可得![]() ,再聯(lián)立
,再聯(lián)立![]() 與C求得二次方程令判別式等于0即可求得
與C求得二次方程令判別式等于0即可求得![]() .
.
(2) 由題意設(shè)直線l的方程為![]() ,聯(lián)立直線l與橢圓的方程,再利用韋達定理與面積公式求得關(guān)于
,聯(lián)立直線l與橢圓的方程,再利用韋達定理與面積公式求得關(guān)于![]() 的面積的表達式,最后利用換元求導(dǎo)分析函數(shù)的最值即可.
的面積的表達式,最后利用換元求導(dǎo)分析函數(shù)的最值即可.
解:(1)依題意,得![]()
將![]() 代入橢圓的方程,得
代入橢圓的方程,得![]()
由![]() ,解得
,解得![]()
所以橢圓的標(biāo)準(zhǔn)方程為![]()
(2)由(1)可得左焦點![]()
由題意設(shè)直線l的方程為![]() ,
,
代入橢圓方程,得![]()
設(shè)![]() ,則
,則![]()
所以![]() ,AB的中點為
,AB的中點為![]()
設(shè)點![]() ,則
,則![]() ,解得
,解得![]()
故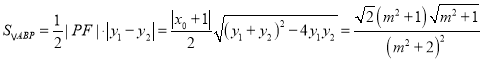
令![]() ,則
,則![]() ,且
,且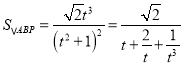
設(shè)![]() ,則
,則![]()
所以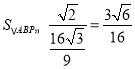 ,即
,即![]() 的面積的最大值為
的面積的最大值為![]()


科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知![]() ,
,![]() ,直線
,直線![]() ,
,![]() 相交于點
相交于點![]() ,且它們的斜率之積是
,且它們的斜率之積是![]() .
.
(1)求點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(2)過點![]() 的直線與軌跡
的直線與軌跡![]() 交于點
交于點![]() ,與
,與![]() 交于點
交于點![]() ,過
,過![]() 作
作![]() 的垂直線交
的垂直線交![]() 軸于點
軸于點![]() ,求證:
,求證:![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】(2016高考新課標(biāo)II,理15)有三張卡片,分別寫有1和2,1和3,2和3.甲,乙,丙三人各取走一張卡片,甲看了乙的卡片后說:“我與乙的卡片上相同的數(shù)字不是2”,乙看了丙的卡片后說:“我與丙的卡片上相同的數(shù)字不是1”,丙說:“我的卡片上的數(shù)字之和不是5”,則甲的卡片上的數(shù)字是________.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知圓![]() ,圓
,圓![]() ,動圓P與圓M外切并且與圓N內(nèi)切,圓心P的軌跡為曲線C.
,動圓P與圓M外切并且與圓N內(nèi)切,圓心P的軌跡為曲線C.
(1)求曲線C的方程;
(2)設(shè)不經(jīng)過點![]() 的直線l與曲線C相交于A,B兩點,直線QA與直線QB的斜率均存在且斜率之和為-2,證明:直線l過定點.
的直線l與曲線C相交于A,B兩點,直線QA與直線QB的斜率均存在且斜率之和為-2,證明:直線l過定點.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,設(shè)拋物線方程為![]() (p>0),M為直線
(p>0),M為直線![]() 上任意一點,過M引拋物線的切線,切點分別為A,B.
上任意一點,過M引拋物線的切線,切點分別為A,B.
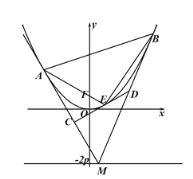
(1)求直線AB與![]() 軸的交點坐標(biāo);
軸的交點坐標(biāo);
(2)若E為拋物線弧AB上的動點,拋物線在E點處的切線與三角形MAB的邊MA,MB分別交于點![]() ,
,![]() ,記
,記![]() ,問
,問![]() 是否為定值?若是求出該定值;若不是請說明理由.
是否為定值?若是求出該定值;若不是請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】全國文明城市是中國所有城市品牌中含金量最高、創(chuàng)建難度最大的一個,是反映城市整體文明水平的綜合性榮譽稱號,是目前國內(nèi)城市綜合類評比中的最高榮譽,也是最具價值的城市品牌,作為普通市民,既是城市文明的最大受益者,更是文明城市的主要創(chuàng)造者,皖北某市為提高市民對文明城市創(chuàng)建的認(rèn)識,舉辦了“創(chuàng)建文明城市”知識競賽,從所有答卷中隨機抽取400份試卷作為樣本,將樣本的成績(滿分100分,成績均為不低于40分的整數(shù))分成六段:![]() 后得到如圖所示的頻率分布直方圖.
后得到如圖所示的頻率分布直方圖.
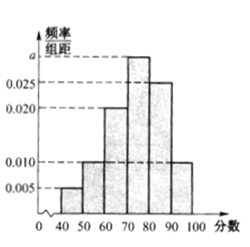
(Ⅰ)求樣本的平均數(shù);
(Ⅱ)現(xiàn)從該樣本成績在![]() 與
與![]() 兩個分?jǐn)?shù)段內(nèi)的市民中按分層抽樣選取6人,求從這6人中隨機選取2人,且2人的競賽成績之差的絕對值大于20的概率.
兩個分?jǐn)?shù)段內(nèi)的市民中按分層抽樣選取6人,求從這6人中隨機選取2人,且2人的競賽成績之差的絕對值大于20的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() :
:![]() (
(![]() )的右焦點為
)的右焦點為![]() ,離心率為
,離心率為![]() .直線
.直線![]() 過點
過點![]() 且不平行于坐標(biāo)軸,
且不平行于坐標(biāo)軸,![]() 與
與![]() 有兩個交點
有兩個交點![]() ,
,![]() ,線段
,線段![]() 的中點為
的中點為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)證明:直線![]() 的斜率與
的斜率與![]() 的斜率的乘積為定值;
的斜率的乘積為定值;
(3)延長線段![]() 與橢圓
與橢圓![]() 交于點
交于點![]() ,若四邊形
,若四邊形![]() 為平行四邊形,求此時直線
為平行四邊形,求此時直線![]() 的斜率.
的斜率.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com