
【題目】某學校的特長班有50名學生,其中有體育生20名,藝術生30名,在學校組織的一次體檢中,該班所有學生進行了心率測試,心率全部介于50次/分到75次/分之間,現(xiàn)將數(shù)據分成五組,第一組![]() ,第二組
,第二組![]() ,…,第五組
,…,第五組![]() ,按上述分組方法得到的頻率分布直方圖如圖所示,已知圖中從左到右的前三組的頻率之比為
,按上述分組方法得到的頻率分布直方圖如圖所示,已知圖中從左到右的前三組的頻率之比為![]() .
.

(Ⅰ)求![]() 的值,并求這50名同學心率的平均值;
的值,并求這50名同學心率的平均值;
(Ⅱ)因為學習專業(yè)的原因,體育生常年進行系統(tǒng)的身體鍛煉,藝術生則很少進行系統(tǒng)的身體鍛煉,若從第一組和第二組的學生中隨機抽取一名,該學生是體育生的概率為0.8,請將下面的列聯(lián)表補充完整,并判斷是否有99.5%的把握認為心率小于60次/分與常年進行系統(tǒng)的身體鍛煉有關?說明你的理由.
參考數(shù)據:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
參考公式:  ,其中
,其中![]()
心率小于60次/分 | 心率不小于60次/分 | 合計 | |
體育生 | 20 | ||
藝術生 | 30 | ||
合計 | 50 |
【答案】(Ⅰ)![]() ,
,![]() ;(Ⅱ)見解析.
;(Ⅱ)見解析.
【解析】試題分析:(1)求出各組的頻數(shù),即可求a的值和50名同學的心率平均值.
(2)列出二聯(lián)表,代入公式求![]() 做出判斷即可.
做出判斷即可.
試題解析:
(Ⅰ)因為第二組數(shù)據的頻率為![]() ,故第二組的頻數(shù)為
,故第二組的頻數(shù)為![]() ,所以第一組的頻數(shù)為
,所以第一組的頻數(shù)為![]() ,第三組的頻數(shù)為20,第四組的頻數(shù)為16,第五組的數(shù)為4.所以
,第三組的頻數(shù)為20,第四組的頻數(shù)為16,第五組的數(shù)為4.所以![]()
![]() ,故
,故![]() .
.
這50名同學的心率平均值為![]()
![]()
![]() .
.
(Ⅱ)由(Ⅰ)知,第一組和第二組的學生(即心率小于60次/分的學生)共10名,從而體育生有![]() 名,故列聯(lián)表補充如下.
名,故列聯(lián)表補充如下.
心率小于60次/分 | 心率不小于60次/分 | 合計 | |
體育生 | 8 | 12 | 20 |
藝術生 | 2 | 28 | 30 |
合計 | 10 | 40 | 50 |
所以![]()
![]() ,
,
故有99.5%的把握認為心率小于60次/分與常年進行系統(tǒng)的身體鍛煉有關.


 時刻準備著暑假作業(yè)原子能出版社系列答案
時刻準備著暑假作業(yè)原子能出版社系列答案科目:高中數(shù)學 來源: 題型:
【題目】一戶居民根據以往的月用電量情況,繪制了月用電量的頻率分布直方圖(月用電量都在25度到325度之間)如圖所示.將月用電量落入該區(qū)間的頻率作為概率.若每月的用電量在200度以內(含200度),則每度電價0.5元,若每月的用電量超過200度,則超過的部分每度電價0.6元.記![]() (單位:度,
(單位:度,![]() )為該用戶下個月的用電量,
)為該用戶下個月的用電量,![]() (單位:元)為下個月所繳納的電費.
(單位:元)為下個月所繳納的電費.
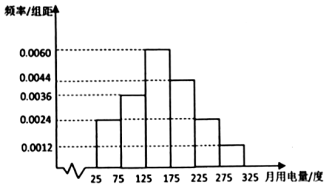
(1)估計該用戶的月用電量的平均值(同一組中的數(shù)據用該組區(qū)間的中點值作代表);
(2)將![]() 表示為
表示為![]() 的函數(shù);
的函數(shù);
(3)根據直方圖估計下個月所繳納的電費![]() 的概率.
的概率.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知命題![]() “存在
“存在![]() ”,命題
”,命題![]() :“曲線
:“曲線![]() 表示焦點在
表示焦點在![]() 軸上的橢圓”,命題
軸上的橢圓”,命題![]() “曲線
“曲線![]() 表示雙曲線”
表示雙曲線”
(1)若“![]() 且
且![]() ”是真命題,求實數(shù)
”是真命題,求實數(shù)![]() 的取值范圍;
的取值范圍;
(2)若![]() 是
是![]() 的必要不充分條件,求實數(shù)
的必要不充分條件,求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)f(x)=x2+(a+8)x+a2+a﹣12(a<0),且f(a2﹣4)=f(2a﹣8),則 ![]() 的最小值為( )
的最小值為( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】設函數(shù)![]() ,
, ![]() (
(![]() ).
).
(1)求函數(shù)![]() 的單調增區(qū)間;
的單調增區(qū)間;
(2)當![]() 時,記
時,記![]() ,是否存在整數(shù)
,是否存在整數(shù)![]() ,使得關于
,使得關于![]() 的不等式
的不等式![]() 有解?若存在,請求出
有解?若存在,請求出![]() 的最小值;若不存在,請說明理由.
的最小值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知橢圓![]() (
(![]() )的離心率為
)的離心率為![]() ,
, ![]() 分別是它的左、右焦點,且存在直線
分別是它的左、右焦點,且存在直線![]() ,使
,使![]() 關于
關于![]() 的對稱點恰好是圓
的對稱點恰好是圓![]() (
(![]() )的一條直線的兩個端點.
)的一條直線的兩個端點.
(1)求橢圓![]() 的方程;
的方程;
(2)設直線![]() 與拋物線
與拋物線![]() (
(![]() )相交于
)相交于![]() 兩點,射線
兩點,射線![]() ,
, ![]() 與橢圓
與橢圓![]() 分別相交于點
分別相交于點![]() ,試探究:是否存在數(shù)集
,試探究:是否存在數(shù)集![]() ,當且僅當
,當且僅當![]() 時,總存在
時,總存在![]() ,使點
,使點![]() 在以線段
在以線段![]() 為直徑的圓內?若存在,求出數(shù)集
為直徑的圓內?若存在,求出數(shù)集![]() ;若不存在,請說明理由.
;若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知過原點的動直線![]() 與圓
與圓![]() 相交于不同的兩點
相交于不同的兩點![]() .
.
(1)求線段![]() 的中點
的中點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(2)是否存在實數(shù)![]() ,使得直線
,使得直線![]() 與曲線
與曲線![]() 只有一個交點?若存在,求出
只有一個交點?若存在,求出![]() 的取值范圍;若不存在,請說明理由.
的取值范圍;若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某保險公司有一款保險產品的歷史收益率(收益率=利潤÷保費收入)的頻率分布直方圖如圖所示:

(Ⅰ)試估計平均收益率;
(Ⅱ)根據經驗,若每份保單的保費在20元的基礎上每增加![]() 元,對應的銷量
元,對應的銷量![]() (萬份)與
(萬份)與![]() (元)有較強線性相關關系,從歷史銷售記錄中抽樣得到如下5組
(元)有較強線性相關關系,從歷史銷售記錄中抽樣得到如下5組![]() 與
與![]() 的對應數(shù)據:
的對應數(shù)據:

據此計算出的回歸方程為![]() .
.
(i)求參數(shù)![]() 的估計值;
的估計值;
(ii)若把回歸方程![]() 當作
當作![]() 與
與![]() 的線性關系,用(Ⅰ)中求出的平均收益率估計此產品的收益率,每份保單的保費定為多少元時此產品可獲得最大收益,并求出該最大收益.
的線性關系,用(Ⅰ)中求出的平均收益率估計此產品的收益率,每份保單的保費定為多少元時此產品可獲得最大收益,并求出該最大收益.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com