
【題目】已知函數![]() .
.
(I) 當![]() 時,求函數
時,求函數![]() 的單調區間;
的單調區間;
(II) 當![]() 時,
時,![]() 恒成立,求
恒成立,求![]() 的取值范圍.
的取值范圍.
【答案】(1)見解析;(2)見解析.
【解析】
試題分析:(Ⅰ)對函數![]() 求導,令
求導,令![]() ,由
,由![]() ,可得
,可得![]() 有兩個不同解,結合函數
有兩個不同解,結合函數![]() 的定義域,即可求得函數
的定義域,即可求得函數![]() 的單調區間;(Ⅱ)當
的單調區間;(Ⅱ)當![]() 時,
時,![]() 恒成立等價于當
恒成立等價于當![]() 時,
時,![]() 恒成立,令
恒成立,令![]() ,求導得
,求導得![]() ,設
,設![]() ,利用導數研究函數
,利用導數研究函數![]() 的單調性,從而可確定
的單調性,從而可確定![]() ,然后對
,然后對![]() 分類討論,即可求得
分類討論,即可求得![]() 的取值范圍.
的取值范圍.
試題解析:(Ⅰ)∵![]() ,函數定義域為:
,函數定義域為:![]()
∴![]()
令![]() ,由
,由![]() 可知,
可知,![]()
從而![]() 有兩個不同解.
有兩個不同解.
令![]() ,則
,則![]()
當![]() 時,
時,![]() ;當
;當![]() 時,
時,![]() ,
,
所以函數![]() 的單調遞增區間為
的單調遞增區間為![]() ,
,
單調遞減區間為![]() .
.
(Ⅱ)由題意得,當![]() 時,
時,![]() 恒成立.
恒成立.
令![]() ,求導得
,求導得![]() ,
,
設![]() ,則
,則![]() ,
,
∵![]()
∴![]()
∴![]() ,
,
∴![]() 在
在![]() 上單調遞增,即
上單調遞增,即![]() 在
在![]() 上單調遞增,
上單調遞增,
∴![]()
①當![]() 時,
時,![]() ,
,
此時,![]() 在
在![]() 上單調遞增,而
上單調遞增,而![]() .
.
∴![]() 恒成立,滿足題意.
恒成立,滿足題意.
②當![]() 時,
時,![]() ,而
,而![]()
根據零點存在性定理可知,存在![]() ,使得
,使得![]() .
.
當![]() 時,
時,![]() 單調遞減;
單調遞減;
當![]() 時,
時,![]() ,
,![]() 單調遞增.
單調遞增.
∴有![]() ,
,
∴![]() 恒成立矛盾
恒成立矛盾
∴實數![]() 的取值范圍為
的取值范圍為![]()


 開心練習課課練與單元檢測系列答案
開心練習課課練與單元檢測系列答案科目:高中數學 來源: 題型:
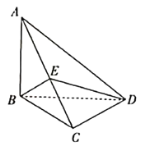
【題目】如圖,在三棱錐![]() 中,
中,![]() 平面
平面![]() ,底面
,底面![]() 是以
是以![]() 為斜邊的等腰直角三角形,
為斜邊的等腰直角三角形,![]() ,
,![]() 是線段
是線段![]() 上一點.
上一點.
(1)若![]() 為
為![]() 的中點,求直線
的中點,求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
(2)是否存在點![]() ,使得平面
,使得平面![]() 平面
平面![]() ?若存在,請指出點
?若存在,請指出點![]() 的位置,并加以證明;若不存在,請說明理由.
的位置,并加以證明;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,以原點
中,以原點![]() 為極點,
為極點,![]() 軸的正半軸為極軸建立極坐標系. 已知曲線的極坐標方程為
軸的正半軸為極軸建立極坐標系. 已知曲線的極坐標方程為![]() ,直線 的參數方程為
,直線 的參數方程為 (
(![]() 為參數).
為參數).
(I)分別求曲線![]() 的直角坐標方程和直線
的直角坐標方程和直線![]() 的普通方程;
的普通方程;
(II)設曲線![]() 和直線
和直線![]() 相交于
相交于![]() 兩點,求弦長
兩點,求弦長![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】閱讀材料:空間直角坐標系O﹣xyz中,過點P(x0,y0,z0)且一個法向量為![]() =(a,b,c)的平面α的方程為a(x﹣x0)+b(y﹣y0)+c(z﹣z0)=0;過點P(x0,y0,z0)且一個方向向量為
=(a,b,c)的平面α的方程為a(x﹣x0)+b(y﹣y0)+c(z﹣z0)=0;過點P(x0,y0,z0)且一個方向向量為![]() =(u,v,w)(uvw≠0)的直線l的方程為
=(u,v,w)(uvw≠0)的直線l的方程為![]() ,閱讀上面材料,并解決下面問題:已知平面α的方程為x+2y﹣2z﹣4=0,直線l是兩平面3x﹣2y﹣7=0與2y﹣z+6=0的交線,則直線l與平面α所成角的大小為( )
,閱讀上面材料,并解決下面問題:已知平面α的方程為x+2y﹣2z﹣4=0,直線l是兩平面3x﹣2y﹣7=0與2y﹣z+6=0的交線,則直線l與平面α所成角的大小為( )
A. arcsin![]() B. arcsin
B. arcsin![]()
C. arcsin![]() D. arcsin
D. arcsin![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】故宮博物院五一期間同時舉辦“戲曲文化展”、“明代御窖瓷器展”、“歷代青綠山水畫展”、 “趙孟頫書畫展”四個展覽.某同學決定在五一當天的上、下午各參觀其中的一個,且至少參觀一個畫展,則不同的參觀方案共有
A. 6種 B. 8種 C. 10種 D. 12種
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一次數學會議中,有五位教師來自![]() 三所學校,其中
三所學校,其中![]() 學校有
學校有![]() 位,
位,![]() 學校有
學校有![]() 位,
位,![]() 學校有
學校有![]() 位。現在五位老師排成一排照相,若要求來自同一學校的老師不相鄰,則共有_______種不同的站隊方法.
位。現在五位老師排成一排照相,若要求來自同一學校的老師不相鄰,則共有_______種不同的站隊方法.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知命題:“若![]() ,則關于x的不等式
,則關于x的不等式![]() 的解集為空集”,那么它的逆命題,否命題,逆否命題,以及原命題中,假命題的個數是( )
的解集為空集”,那么它的逆命題,否命題,逆否命題,以及原命題中,假命題的個數是( )
A.0B.2C.3D.4
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com