
【題目】(本小題滿分14分)
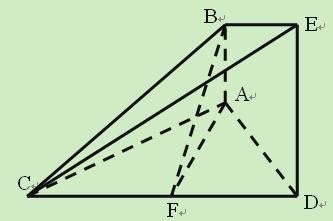
如圖的幾何體中, ![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,△
,△![]() 為等邊三角形
為等邊三角形![]() ,
, ![]() 為
為![]() 的中點.
的中點.
(1)求證: ![]() 平面
平面![]() ;
;
(2)求證:平面![]() 平面
平面![]() 。
。
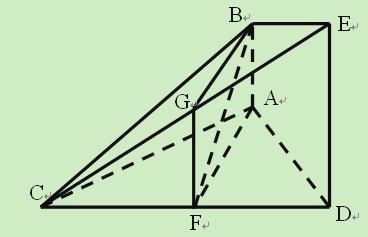
【答案】(1)證明:取![]() 的中點
的中點![]() ,連結
,連結![]() .
.
∵![]() 為
為![]() 的中點,∴
的中點,∴![]() 且
且![]() .
.
∵![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
∴![]() ,∴
,∴![]() .
.
又![]() ,∴
,∴![]() . …………3分
. …………3分
∴四邊形![]() 為平行四邊形,則
為平行四邊形,則![]() .……………5分
.……………5分
∵![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() .…………7分
.…………7分
(2)證明:∵![]() 為等邊三角形,
為等邊三角形, ![]() 為
為![]() 的中點,∴
的中點,∴![]() …………9分
…………9分
∵![]() 平面
平面![]() ,
, ![]() ,∴
,∴![]() .……………10分
.……………10分
又![]() ,∴
,∴![]() 平面
平面![]() .……………………………12分
.……………………………12分
∵![]() ,∴
,∴![]() 平面
平面![]() .…………………………………13分
.…………………………………13分
∵![]() 平面
平面![]() ,∴平面
,∴平面![]() 平面
平面![]() .………………14分
.………………14分
【解析】試題分析:(1)通過取![]() 的中點
的中點![]() ,利用三角形的中位線定理和平行四邊形的性質及線面平行的判定定理即可證明;(2)連接
,利用三角形的中位線定理和平行四邊形的性質及線面平行的判定定理即可證明;(2)連接![]() ,設
,設![]() 到平面
到平面![]() 的距離為
的距離為![]() ,利用等體積法
,利用等體積法![]() 可求得結果.
可求得結果.
試題解析:(1)證明:取![]() 的中點
的中點![]() ,連接
,連接![]() 、
、![]() .
.
∵![]() 為
為![]() 的中點,∴
的中點,∴![]() 且
且![]() .
.
∵![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
∴![]() ,∴
,∴![]() ,
,
又![]() ,∴
,∴![]() .
.
∴四邊形![]() 為平行四邊形,則
為平行四邊形,則![]() .
.
∵![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() .
.
(2)連接![]() ,設
,設![]() 到平面
到平面![]() 的距離為
的距離為![]() ,
,
在![]() 中,
中, ![]() ,
, ![]() ,
,
∴![]() ,
,
又![]() ,
, ![]() ,
,
∴由![]() ,即
,即![]() (
(![]() 為正
為正![]() 的高),
的高),
∴![]()
即點![]() 到平面
到平面![]() 的距離為
的距離為![]() .
.


科目:高中數學 來源: 題型:
【題目】某醫學院讀書協會欲研究晝夜溫差大小與患感冒人數多少之間的關系,該協會分別到氣象局與某醫院抄錄了1至6月份每月10號的晝夜溫差情況與因患感冒而就診的人數,得到如下頻數分布直方圖:
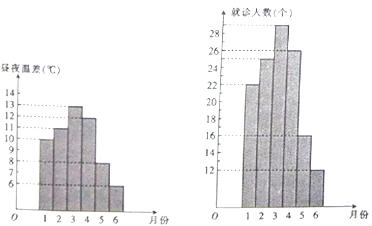
該協會確定的研究方案是:先從這六組數據中選取2組,用剩下的4組數據求線性回歸方程,再用被選取的2組數據進行檢驗.
(1)求選取的2組數據恰好是相鄰兩個月的頻率;
(2)已知選取的是1月與6月的兩組數據.
(i)請根據2至5月份的數據,求出就診人數![]() 關于晝夜溫差
關于晝夜溫差![]() 的線性回歸方程;
的線性回歸方程;
(ii)若由線性回歸方程得到的估計數據與所選出的檢驗數據的誤差均不超過2人,則認為得到的線性回歸方程是理想的,試問該協會所得線性回歸方程是否理想?
(參考公式: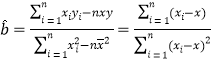 ,
,![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某民調機構為了了解民眾是否支持英國脫離歐盟,隨機抽調了100名民眾,他們的年齡的頻數及支持英國脫離歐盟的人數分布如下表:
年齡段 | 18-24歲 | 25-49歲 | 50-64歲 | 65歲及以上 |
頻數 | 35 | 20 | 25 | 20 |
支持脫歐的人數 | 10 | 10 | 15 | 15 |
(Ⅰ)由以上統計數據填下面列聯表,并判斷是否有99%的把握認為以50歲胃分界點對是否支持脫離歐盟的態度有差異;
年齡低于50歲的人數 | 年齡不低于50歲的人數 | 合計 | |
支持“脫歐”人數 | |||
不支持“脫歐”人數 | |||
合計 |
附:![]()

(Ⅱ)若采用分層抽樣的方式從18-64歲且支持英國脫離歐盟的民眾中選出7人,再從這7人中隨機選出2人,求這2人至少有1人年齡在18-24歲的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】定義在![]() 上的函數
上的函數![]() ,如果滿足:對任意
,如果滿足:對任意![]() ,存在常數
,存在常數![]() ,都有
,都有![]() 成立,則稱
成立,則稱![]() 是
是![]() 上的有界函數,其中
上的有界函數,其中![]() 稱為函數
稱為函數![]() 的上界,已知函數
的上界,已知函數![]() .
.
(1)當![]() 時,求函數
時,求函數![]() 在
在![]() 上的值域,并判斷函數
上的值域,并判斷函數![]() 在
在![]() 上是否為有界函數,請說明理由;
上是否為有界函數,請說明理由;
(2)若函數![]() 在
在![]() 上是以4為上界的有界函數,求實數
上是以4為上界的有界函數,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】近年來,“共享單車”的出現為市民“綠色出行”提供了極大的方便,某共享單車公司“Mobike”計劃在甲、乙兩座城市共投資120萬元,根據行業規定,每個城市至少要投資40萬元,由前期市場調研可知:甲城市收益![]() 與投入
與投入![]() (單位:萬元)滿足
(單位:萬元)滿足![]() ,乙城市收益
,乙城市收益![]() 與投入
與投入![]() (單位:萬元)滿足
(單位:萬元)滿足![]() ,設甲城市的投入為
,設甲城市的投入為![]() (單位:萬元),兩個城市的總收益為
(單位:萬元),兩個城市的總收益為![]() (單位:萬元)。
(單位:萬元)。
(1)當甲城市投資50萬元時,求此時公司總收益;
(2)試問如何安排甲、乙兩個城市的投資,才能使總收益最大?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,菱形ABCD的對角線AC與BD交于點O,點E,F分別在AD,CD上,AE=CF,EF交BD于點H.將△DEF沿EF折到△D′EF的位置.
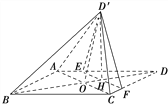
(1)證明:AC⊥HD′;
(2)若AB=5,AC=6,AE=![]() ,OD′=2
,OD′=2![]() ,求五棱錐D′ABCFE的體積.
,求五棱錐D′ABCFE的體積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com