
【題目】已知圓C的極坐標方程為![]() ,直線
,直線![]() 的參數方程為
的參數方程為![]() .若直線
.若直線![]() 與圓C相交于不同的兩點P,Q.
與圓C相交于不同的兩點P,Q.
(Ⅰ)寫出圓C的直角坐標方程,并求圓心的坐標與半徑;
(Ⅱ)若弦長|PQ|=4,求直線![]() 的斜率.
的斜率.
【答案】(1)(x﹣2)2+(y+3)2=13,圓心為(2,﹣3),半徑為![]() (2)0或
(2)0或![]()
【解析】試題分析:(Ⅰ)兩邊同乘以![]() 利用
利用![]() 可寫出圓
可寫出圓![]() 的直角坐標方程,并求出圓心的坐標與半徑;(Ⅱ)將直線參數方程和的直線過定點根據點斜式可得直線方程為
的直角坐標方程,并求出圓心的坐標與半徑;(Ⅱ)將直線參數方程和的直線過定點根據點斜式可得直線方程為![]() ,代入圓的直角坐標方程,根據弦長
,代入圓的直角坐標方程,根據弦長![]() 以及點到直線的距離公式可得以
以及點到直線的距離公式可得以![]() ,從而可求直線
,從而可求直線![]() 的斜率.
的斜率.
試題解析:
解:(Ⅰ)由![]() ,得圓C直角坐標方程x2+y2﹣4x+6y=0,配方,得(x﹣2)2+(y+3)2=13,所以圓心為(2,﹣3),半徑為
,得圓C直角坐標方程x2+y2﹣4x+6y=0,配方,得(x﹣2)2+(y+3)2=13,所以圓心為(2,﹣3),半徑為![]()
(Ⅱ)由直線![]() 的參數方程知直線過定點M(4,0),則由題意,知直線l的斜率一定存在,
的參數方程知直線過定點M(4,0),則由題意,知直線l的斜率一定存在,
設直線![]() 的方程為y=k(x﹣4),因為弦長|PQ|=4,所以
的方程為y=k(x﹣4),因為弦長|PQ|=4,所以![]() =3,
=3,
解得k=0或k=﹣![]()


 53隨堂測系列答案
53隨堂測系列答案科目:高中數學 來源: 題型:
【題目】2017年春節期間,某服裝超市舉辦了一次有獎促銷活動,消費每超過600元(含600元),均可抽獎一次,抽獎方案有兩種,顧客只能選擇其中的一種.
方案一:從裝有10個形狀、大小完全相同的小球(其中紅球3個,黑球7個)的抽獎盒中,一次性摸出3個球,其中獎規則為:若摸到3個紅球,享受免單優惠;若摸出2個紅球則打6折,若摸出1個紅球,則打7折;若沒摸出紅球,則不打折.
方案二:從裝有10個形狀、大小完全相同的小球(其中紅球3個,黑球7個)的抽獎盒中,有放回每次摸取1球,連摸3次,每摸到1次紅球,立減200元.
(1)若兩個顧客均分別消費了600元,且均選擇抽獎方案一,試求兩位顧客均享受免單優惠的概率;
(2)若某顧客消費恰好滿1000元,試從概率的角度比較該顧客選擇哪一種抽獎方案更合算?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】第![]() 屆夏季奧林匹克運動會將于 2016 年 8 月 5 日—21 日在巴西里約熱內盧舉行.下表是近五屆奧運會中國代表團和俄羅斯代表團獲得的金牌數的統計數據( 單位: 枚).
屆夏季奧林匹克運動會將于 2016 年 8 月 5 日—21 日在巴西里約熱內盧舉行.下表是近五屆奧運會中國代表團和俄羅斯代表團獲得的金牌數的統計數據( 單位: 枚).
第 | 第 | 第 | 第 | 第 | |
中國 |
|
|
|
|
|
俄羅斯 |
|
|
|
|
|
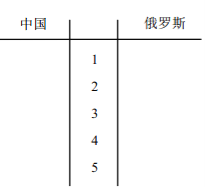
(1)根據表格中兩組數據完成近五屆奧運會兩國代表團獲得的金牌數的莖葉圖, 并通過莖葉圖比較兩國代表團獲得的金牌數的平均值及分散程度( 不要求計算出具體數值, 給出結論即可);
(2)甲、 乙、 丙三人競猜今年中國代表團和俄羅斯代表團中的哪一個獲得的金牌數多( 假設兩國代表團獲得的金牌數不會相等) , 規定甲、 乙、 丙必須在兩個代表團中選一個, 已知甲、 乙猜中國代表團的概率都為![]() , 丙猜中國代表團的概率為
, 丙猜中國代表團的概率為![]() , 三人各自猜哪個代表團的結果互不影響.現讓甲、 乙、 丙各猜一次, 設三人中猜中國代表團的人數為
, 三人各自猜哪個代表團的結果互不影響.現讓甲、 乙、 丙各猜一次, 設三人中猜中國代表團的人數為![]() ,求
,求![]() 的分布列及數學期望
的分布列及數學期望![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為加快新能源汽車產業發展,推進節能減排,國家鼓勵消費者購買新能源汽車,某校研究性學習小組,從汽車市場上隨機選取了![]() 輛純電動乘用車,根據其續駛里程
輛純電動乘用車,根據其續駛里程![]() (單次充電后能行駛的最大里程)作出了頻率與頻數的統計表:
(單次充電后能行駛的最大里程)作出了頻率與頻數的統計表:
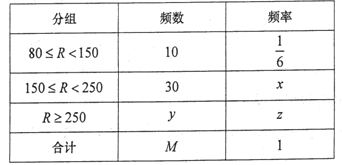
(1)求![]() 的值;
的值;
(2)若用分層抽樣的方法從這![]() 輛純電動乘用車中抽取一個容量為6的樣本,從該樣本中任選2輛,求選到的2輛車續駛里程為
輛純電動乘用車中抽取一個容量為6的樣本,從該樣本中任選2輛,求選到的2輛車續駛里程為![]() 的概率.
的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知f(x)是定義在R上的偶函數,且x≤0時,f(x)=log![]() (-x+1).
(-x+1).
(1)求f(0),f(1);
(2)求函數f(x)的解析式;
(3)若f(a-1)<-1,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了研究家用轎車在高速公路上的車速情況,交通部門隨機對50名家用轎車駕駛員進行調查,得到其在高速公路上行駛時的平均車速情況為:在30名男性駕駛員中,平均車速超過![]() 的有20人,不超過
的有20人,不超過![]() 的有10人.在20名女性駕駛員中,平均車速超過
的有10人.在20名女性駕駛員中,平均車速超過![]() 的有5人,不超過
的有5人,不超過![]() 的有15人.
的有15人.
(Ⅰ)完成下面的列聯表,并判斷是否有99.5%的把握認為平均車速超過![]() 的人與性別有關;
的人與性別有關;
平均車速超過
| 平均車速不超過
| 合計 | |
男性駕駛員人數 | |||
女性駕駛員人數 | |||
合計 |
(Ⅱ )以上述數據樣本來估計總體,現從高速公路上行駛的大量家用轎車中隨機抽取3輛,記這3輛車中駕駛員為女性且車速不超過![]() 的車輛數為
的車輛數為![]() ,若每次抽取的結果是相互獨立的,求
,若每次抽取的結果是相互獨立的,求![]() 的分布列和數學期望.
的分布列和數學期望.
參考公式: ![]() ,其中
,其中![]() .
.
參考數據:
| 0.150 | 0.100 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設A是同時符合以下性質的函數f(x)組成的集合:
①x∈[0,+∞),都有f(x)∈(1,4];②f(x)在[0,+∞)上是減函數.
(1)判斷函數f1(x)=2-![]() 和f2(x)=1+3·
和f2(x)=1+3·![]() (x≥0)是否屬于集合A,并簡要說明理由;
(x≥0)是否屬于集合A,并簡要說明理由;
(2)把(1)中你認為是集合A中的一個函數記為g(x),若不等式g(x)+g(x+2)≤k對任意的x≥0總成立,求實數k的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在某校組織的“共筑中國夢”競賽活動中,甲、乙兩班各有6名選手參賽,在第一輪筆試環節中,評委將他們的筆試成績作為樣本數據,繪制成如圖所示的莖葉圖,為了增加結果的神秘感,主持人故意沒有給出甲、乙兩班最后一位選手的成績,知識告知大家,如果某位選手的成績高于90分(不含90分),則直接“晉級”.

(1)求乙班總分超過甲班的概率;
(2)主持人最后宣布:甲班第六位選手的得分是90分,乙班第六位選手的得分是97分,
①請你從平均分和方差的角度來分析兩個班的選手的情況;
②主持人從甲乙兩班所有選手成績中分別隨機抽取2個,記抽取到“晉級”選手的總人數為![]() ,求
,求![]() 的分布列及數學期望.
的分布列及數學期望.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com