
【題目】已知t為實數,函數![]() ,其中
,其中![]()
(1)若![]() ,求
,求![]() 的取值范圍。
的取值范圍。
(2)當![]() 時,
時,![]() 的圖象始終在
的圖象始終在![]() 的圖象的下方,求t的取值范圍;
的圖象的下方,求t的取值范圍;
(3)設![]() ,當
,當![]() 時,函數
時,函數![]() 的值域為
的值域為![]() ,若
,若![]() 的最小值為
的最小值為![]() ,求實數a的值.
,求實數a的值.
【答案】(1)![]() (2)t>1(3)a=
(2)t>1(3)a=![]()
【解析】
(1)根據對數函數的圖像與性質化簡即可求解;
(2)構造函數h(x)=f(x)-g(x),根據對數函數的圖象和性質可得,根據二次函數的性質求出t的取值范圍即可;
(3)先判斷函數y=|f(x)|的單調性,令|2loga(2x+2)|=2,即可得到n-m的最小值.
解:(1)由題意得函數g(x)在(0,+∞)上是減函數,
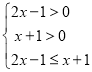 ,解得
,解得![]() ,則x的取值范圍是
,則x的取值范圍是![]() ;
;
(2)由題意設h(x)=f(x)-g(x)=2loga(2x+t-2)-logax<0在x∈[1,4]恒成立,
∴2loga(2x+t-2)<logax,
∵0<a<1,x∈[1,4],
∴只需要2x+t-2>![]() 恒成立,
恒成立,
即![]() 恒成立,
恒成立,
∴![]() ,
,
令![]() ,
,
∴![]() ,
,
∴t的取值范圍是t>1,
(3)∵t=4,0<a<1,
∴函數y=|f(x)|=|2loga(2x+2)|在(-1,-![]() )上單調遞減,在(-
)上單調遞減,在(-![]() ,+∞)上單調遞增,
,+∞)上單調遞增,
∵當x∈[m,n]時,函數y=|f(x)|的值域為[0,2],且f(-![]() )=0,
)=0,
∴![]() (等號不同時取到),
(等號不同時取到),
令|2loga(2x+2)|=2,得![]() ,
,
又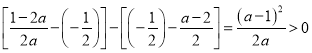 ,
,
∴![]() ,
,
∴n-m的最小值為![]() ,
,
∴a=![]() .
.


 啟東小題作業本系列答案
啟東小題作業本系列答案科目:高中數學 來源: 題型:
【題目】某城市理論預測2010年到2014年人口總數與年份的關系如下表所示
年份2010+x(年) | 0 | 1 | 2 | 3 | 4 |
人口數y(十萬) | 5 | 7 | 8 | 11 | 19 |
(1)請根據上表提供的數據,求出y關于x的線性回歸方程;
(2) 據此估計2015年該城市人口總數。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知 f(x)= ![]() sin2x﹣2sin2x,
sin2x﹣2sin2x,
(1)求f(x)的最小正周期和單調遞減區間;
(2)若x∈[﹣ ![]() ,
, ![]() ],求f(x)的最大值及取得最大值時對應的x的取值.
],求f(x)的最大值及取得最大值時對應的x的取值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】定義在![]() 上的函數
上的函數![]() ,若已知其在
,若已知其在![]() 內只取到一個最大值和一個最小值,且當
內只取到一個最大值和一個最小值,且當![]() 時函數取得最大值為
時函數取得最大值為![]() ;當
;當![]() ,函數取得最小值為
,函數取得最小值為![]() .
.
(1)求出此函數的解析式;
(2)是否存在實數![]() ,滿足不等式
,滿足不等式![]() ?若存在,求出
?若存在,求出![]() 的范圍(或值),若不存在,請說明理由;
的范圍(或值),若不存在,請說明理由;
(3)若將函數![]() 的圖像保持橫坐標不變縱坐標變為原來的
的圖像保持橫坐標不變縱坐標變為原來的![]() 得到函數
得到函數![]() ,再將函數
,再將函數![]() 的圖像向左平移
的圖像向左平移![]() 個單位得到函數
個單位得到函數![]() ,已知函數
,已知函數![]() 的最大值為
的最大值為![]() ,求滿足條件的
,求滿足條件的![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】將函數f(x)= ![]() sin2x﹣
sin2x﹣ ![]() cos2x+1的圖象向左平移
cos2x+1的圖象向左平移 ![]() 個單位,再向下平移1個單位,得到函數y=g(x)的圖象,則下列關予函數y=g(x)的說法錯誤的是( )
個單位,再向下平移1個單位,得到函數y=g(x)的圖象,則下列關予函數y=g(x)的說法錯誤的是( )
A.函數y=g(x)的最小正周期為π
B.函數y=g(x)的圖象的一條對稱軸為直線x= ![]()
C.![]() g(x)dx=
g(x)dx= ![]()
D.函數y=g(x)在區間[ ![]() ,
, ![]() ]上單調遞減
]上單調遞減
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知平面ADC∥平面A1B1C1 , B為線段AD的中點,△ABC≈△A1B1C1 , 四邊形ABB1A1為正方形,平面AA1C1C丄平面ADB1A1 , A1C1=A1A,∠C1A1A= ![]() ,M為棱A1C1的中點.
,M為棱A1C1的中點.
(Ⅰ)若N為線段DC1上的點,且直線MN∥平面ADB1A1 , 試確定點N的位置;
(Ⅱ)求平面MAD與平面CC1D所成的銳二面角的余弦值.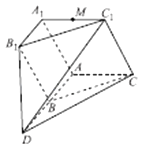
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C: ![]() (a>b>0)的離心率為
(a>b>0)的離心率為 ![]() ,直線l:y=x+2與以原點為圓心、橢圓C的短半軸為半徑的圓O相切.
,直線l:y=x+2與以原點為圓心、橢圓C的短半軸為半徑的圓O相切.
(1)求橢圓C的方程;
(2)過橢圓C的左頂點A作直線m,與圓O相交于兩點R,S,若△ORS是鈍角三角形,求直線m的斜率k的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com