
【題目】已知焦點在![]() 軸上的拋物線
軸上的拋物線![]() 過點
過點![]() ,橢圓
,橢圓![]() 的兩個焦點分別為
的兩個焦點分別為![]() ,其中
,其中![]() 與
與![]() 的焦點重合,過
的焦點重合,過![]() 與長軸垂直的直線交橢圓
與長軸垂直的直線交橢圓![]() 于
于![]() 兩點且
兩點且![]() ,曲線
,曲線![]() 是以原點為圓心以
是以原點為圓心以![]() 為半徑的圓.
為半徑的圓.
(1)求![]() 與
與![]() 及
及![]() 的方程;
的方程;
(2)若動直線![]() 與圓
與圓![]() 相切,且與
相切,且與![]() 交與
交與![]() 兩點,三角形
兩點,三角形![]() 的面積為
的面積為![]() ,求
,求![]() 的取值范圍.
的取值范圍.
【答案】(1)![]()
![]()
![]() ; (2)
; (2)![]() .
.
【解析】
(1)先利用點的坐標求拋物線的方程,再根據題意分別求出橢圓和圓的方程;
(2)設出直線方程,求出面積的表達式,根據表達式的特點,求出范圍.
(1)由已知設拋物線方程為![]() 則
則![]() ,解得
,解得![]() ,
,
即![]() 的方程為
的方程為![]() ;焦點坐標為
;焦點坐標為![]() ,
,
所以橢圓中![]() ,其焦點也在
,其焦點也在![]() 軸上設方程為
軸上設方程為![]()
由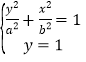 得
得![]() ,
, ![]() 又
又![]() 解得
解得![]()
橢圓方程為![]() ,
,
又![]() 所以所求圓的方程為
所以所求圓的方程為![]() ,
,
(2) 因為直線![]() 與圓
與圓![]() 相切,所以圓心O到直線的距離為1,
相切,所以圓心O到直線的距離為1,
所以![]() ,
,
當直線![]() 的斜率不存在時方程為
的斜率不存在時方程為![]() ,兩種情況所得到的三角形
,兩種情況所得到的三角形![]() 面積相等,
面積相等,
由 得
得![]() ,不妨設
,不妨設![]() ,
, ![]()
此時 ![]() ,
,
當直線![]() 的斜率存在時設為
的斜率存在時設為![]() ,直線方程為
,直線方程為![]()
所以圓心O到直線的距離為![]() 即
即![]() ,
,
由 得
得![]()
所以![]()
![]()
![]() 恒大于0,
恒大于0,
設![]() 則
則![]()
所以![]()
![]()
![]()
![]() ,
,
令![]() 則
則![]() ,
,![]()
所以![]()
![]() 是關于
是關于![]() 的二次函數開口向下,在
的二次函數開口向下,在![]() 時單調遞減,
時單調遞減,
所以![]() ,綜上:
,綜上: ![]() .
.


科目:高中數學 來源: 題型:
【題目】畢業季有![]() 位好友欲合影留念,現排成一排,如果:
位好友欲合影留念,現排成一排,如果:
(1)![]() 、
、![]() 兩人不排在一起,有幾種排法?
兩人不排在一起,有幾種排法?
(2)![]() 、
、![]() 兩人必須排在一起,有幾種排法?
兩人必須排在一起,有幾種排法?
(3)![]() 不在排頭,
不在排頭,![]() 不在排尾,有幾種排法?
不在排尾,有幾種排法?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】現有一段長度為![]() 的木棍,希望將其鋸成盡可能多的小段,要求每一小段的長度都是整數,并且任何一個時刻,當前最長的一段都嚴格小于當前最短的一段長度的2倍,記對
的木棍,希望將其鋸成盡可能多的小段,要求每一小段的長度都是整數,并且任何一個時刻,當前最長的一段都嚴格小于當前最短的一段長度的2倍,記對![]() 符合條件時的最多小段數為
符合條件時的最多小段數為![]() ,則( )。
,則( )。
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】 山東省《體育高考方案》于2012年2月份公布,方案要求以學校為單位進行體育測試,某校對高三1班同學按照高考測試項目按百分制進行了預備測試,并對50分以上的成績進行統計,其頻率分布直方圖如圖所示,若90~100分數段的人數為2人.
(Ⅰ)請估計一下這組數據的平均數M;
(Ⅱ)現根據初賽成績從第一組和第五組(從低分段到高分段依次為第一組、第二組、…、第五組)中任意選出兩人,形成一個小組.若選出的兩人成績差大于20,則稱這兩人為“幫扶組”,試求選出的兩人為“幫扶組”的概率.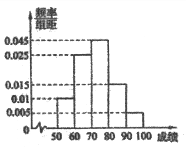
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】趙爽是我國古代數學家、天文學家,大約在公元222年,趙爽為《周髀算經》一書作序時,介紹了“勾股圓方圖”,亦稱“趙爽炫圖”(以弦為邊長得到的正方形組成).類比“趙爽弦圖”,可類似地構造如下圖所示的圖形,它是由3個全等的三角形與中間的一個小等邊三角形拼成的一個大等邊三角形,設![]() ,若在大等邊三角形中隨機取一點,則此點取自小等邊三角形的概率是__________.
,若在大等邊三角形中隨機取一點,則此點取自小等邊三角形的概率是__________.
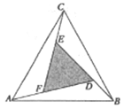
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在四棱錐P-ABCD中,底面ABCD為直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() ,且平面
,且平面![]() 平面ABCD.
平面ABCD.
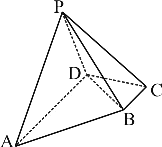
(1)求證:![]() ;
;
(2)在線段PA上是否存在一點M,使二面角M-BC-D的大小為![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com