
【題目】設函數![]() .
.
(1)求函數![]() 的單調區間;
的單調區間;
(2)若![]() ,證明:對任意的實數
,證明:對任意的實數![]() ,都有
,都有![]() .
.
【答案】(1)當![]() 時,
時,![]() 在
在![]() 上單調遞增;當
上單調遞增;當![]() 時,
時,![]() 的單調減區間為
的單調減區間為![]() ,單調增區間為
,單調增區間為![]() ;(2)見解析.
;(2)見解析.
【解析】試題分析:(Ⅰ)求出函數的導數,通過討論![]() 的范圍求出函數的單調區間即可;
的范圍求出函數的單調區間即可;
(Ⅱ)問題轉化為證明![]() ,先證出
,先證出![]() ,再證明
,再證明![]() 令
令![]() ,根據函數的單調性證明即可.
,根據函數的單調性證明即可.
試題解析:(1)定義域為![]() ,
,![]() ,
,
①當![]() 時,
時,![]() ,
,![]() 在
在![]() 上單調遞增,
上單調遞增,
②當![]() 時,令
時,令![]() ,有
,有![]() ,
,
|
|
|
|
|
| 0 |
|
| ↘ | 極小值 | ↗ |
所以![]() 的單調減區間為
的單調減區間為![]() ,單調增區間為
,單調增區間為![]() .
.
綜合①②,當![]() 時,
時,![]() 在
在![]() 上單調遞增;當
上單調遞增;當![]() 時,
時,![]() 的單調減區間為
的單調減區間為![]() ,單調增區間為
,單調增區間為![]() .
.
(2)要證明![]() ,即證明
,即證明![]() ,
,
下面先證明:![]() ,
,
構造函數![]() ,
,![]() ,
,
令![]() 得
得![]() ,當
,當![]() 時,
時,![]() 即
即![]() 在
在![]() 上單調遞增,
上單調遞增,
∴![]() ,
,
于是有![]() ,
,![]() ,
,
∴當![]() 時,
時,![]() ,
,
從而![]() .
.
接下來只需證:![]() ,
,
即證:![]() ,
,
令![]() ,則
,則![]() ,
,
所以![]() 在
在![]() 上單調遞減,
上單調遞減,![]() 上單調遞增,
上單調遞增,
即![]() ,
,
∵![]() 時,
時,![]() ,
,
∴![]() ,
,
∴![]() .
.
點晴:本題主要考查函數單調性,及不等式的證明問題.要求單調性,求導比較導方程的根的大小,解不等式可得單調區間,要證明不等式恒成立問題可轉化為構造新函數證明新函數單調,只需要證明其導函數大于等于0(或者恒小于等于0即可),要證明一個不等式,我們可以先根據題意構造新函數,求其值最值即可.這類問題的通解方法就是:劃歸與轉化之后,就可以假設相對應的函數,然后利用導數研究這個函數的單調性、極值和最值,圖像與性質,進而求解得結果.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】某商店會員活動日.
(Ⅰ)隨機抽取50名會員對商場進行綜合評分,繪制頻率分布直方圖(如圖所示),其中樣本數據分組區間為[40,50),[50,60),…,[80,90),[90,100].
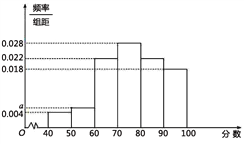
(1)求頻率分布直方圖中的值;
(2)估計會員對商場的評分不低于80的概率.
(Ⅱ)采取摸球兌獎的方式對會員進行返代金券活動,每位會員從一個裝有5個標有面值的球(2個所標的面值為300元,其余3個均為100元)的袋中一次性隨機摸出2個球,球上所標的面值之和為該會員所獲的代金券金額.求某會員所獲得獎勵超過400元的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲、乙兩人約定在中午12時到下午1時之間到某站乘公共汽車,又知這段時間內有4班公共汽車.設到站時間分別為12:15,12:30,12:45,1:00.如果他們約定:
①見車就乘;
②最多等一輛.
試分別求出在兩種情況下兩人同乘一輛車的概率.假設甲乙兩人到達車站的時間是相互獨立的,且每人在中午12點到1點的任意時刻到達車站是等可能的.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】A,B兩名同學在5次數學考試中的成績統計如下面的莖葉圖所示,若A,B兩人的平均成績分別是xA , xB , 觀察莖葉圖,下列結論正確的是( ) 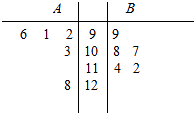
A.xA<xB , B比A成績穩定
B.xA>xB , B比A成績穩定
C.xA<xB , A比B成績穩定
D.xA>xB , A比B成績穩定
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某學校一個生物興趣小組對學校的人工湖中養殖的某種魚類進行觀測研究,在飼料充足的前提下,興趣小組對飼養時間x(單位:月)與這種魚類的平均體重y(單位:千克)得到一組觀測值,如下表:
xi(月) | 1 | 2 | 3 | 4 | 5 |
yi(千克) | 0.5 | 0.9 | 1.7 | 2.1 | 2.8 |
(參考公式: ![]() =
= 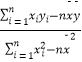 ,
, ![]() =
= ![]() ﹣
﹣ ![]()
![]() )
)
(1)在給出的坐標系中,畫出關于x,y兩個相關變量的散點圖.
(2)請根據上表提供的數據,用最小二乘法求出變量y關于變量x的線性回歸直線方程 ![]() .
.
(3)預測飼養滿12個月時,這種魚的平均體重(單位:千克)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】求適合下列條件的橢圓的標準方程:
(1)以(0,5)和(0,-5)為焦點,且橢圓上一點P到兩焦點的距離之和為26;
(2)以橢圓9x2+5y2=45的焦點為焦點,且經過M(2, ![]() ).
).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在△ABC中,若sinA+sinB=sinC(cosA+cosB).
(1)判斷△ABC的形狀;
(2)在上述△ABC中,若角C的對邊c=1,求該三角形內切圓半徑的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com