
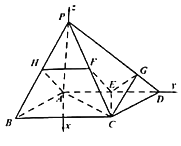
【題目】如圖,在四棱錐![]() 中,
中,![]() 平面
平面![]() ,四邊形
,四邊形![]() 為菱形,
為菱形,![]() ,
,![]() ,E,F分別為
,E,F分別為![]() ,
,![]() 的中點(diǎn).
的中點(diǎn).
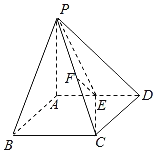
(1)求證:![]() 平面
平面![]() ;
;
(2)點(diǎn)G是線段![]() 上一動(dòng)點(diǎn),若
上一動(dòng)點(diǎn),若![]() 與平面
與平面![]() 所成最大角的正切值為
所成最大角的正切值為![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)證明見解析(2)![]()
【解析】
(1)取![]() 的中點(diǎn)H,連結(jié)
的中點(diǎn)H,連結(jié)![]() ,證明四邊形
,證明四邊形![]() 為平行四邊形得到證明.
為平行四邊形得到證明.
(2)連結(jié)![]() ,證明
,證明![]() 為
為![]() 與平面
與平面![]() 所成角的平面角得到
所成角的平面角得到![]() ,以A為原點(diǎn),如圖建立空間直角坐標(biāo)系,平面
,以A為原點(diǎn),如圖建立空間直角坐標(biāo)系,平面![]() 的一個(gè)法向量為
的一個(gè)法向量為![]() ,平面
,平面![]() 的法向量
的法向量![]() ,計(jì)算夾角得到答案.
,計(jì)算夾角得到答案.
(1)取![]() 的中點(diǎn)H,連結(jié)
的中點(diǎn)H,連結(jié)![]() ,
,
∵E,F分別為![]() 的中點(diǎn),∴
的中點(diǎn),∴![]() ,
,![]() ,
,
由題知![]() ,
,![]() ,∴
,∴![]() ,
,![]() ,
,
∴四邊形![]() 為平行四邊形,∴
為平行四邊形,∴![]() ,
,
∵![]() 平面
平面![]() ,且
,且![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() .
.
(2)連結(jié)![]() ,∵四邊形
,∵四邊形![]() 為菱形,
為菱形,![]() ,
,
∴![]() 是等邊三角形,E為
是等邊三角形,E為![]() 中點(diǎn),
中點(diǎn),
∴![]() ,且
,且![]() ,
,
∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,∴
,∴![]() ,
,![]() ,
,
∴![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]() ,∴
,∴![]() ,
,
∴![]() 為
為![]() 與平面
與平面![]() 所成角的平面角,
所成角的平面角,
在![]() 中,∵
中,∵![]() ,
,
∴當(dāng)![]() 最短時(shí),
最短時(shí),![]() 最大,
最大,![]() ,
,
∵![]() ,∴
,∴![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,∴
,∴![]() ,
,
以A為原點(diǎn),如圖建立空間直角坐標(biāo)系,
則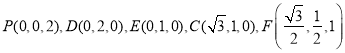 ,
,
則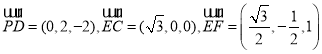 ,
,
∵![]() ,∴
,∴![]() 平面
平面![]() ,
,
∴平面![]() 的一個(gè)法向量為
的一個(gè)法向量為![]() ,
,
平面![]() 的法向量
的法向量![]() ,
,
則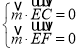 ,∴
,∴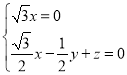 ,取
,取![]() ,得
,得![]() ,
,
設(shè)二面角![]() 的平面角為
的平面角為![]() ,
,
則![]() ,
,
∴二面角![]() 的余弦值為
的余弦值為![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學(xué)生10分鐘應(yīng)用題系列答案
小學(xué)生10分鐘應(yīng)用題系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知數(shù)列{an}中,相鄰兩項(xiàng)an,an+1是關(guān)于x的方程:x2+3nx+bn![]() 0(n∈N*)的兩實(shí)根,且a1=1.
0(n∈N*)的兩實(shí)根,且a1=1.
(1)若Sn為數(shù)列{an}的前n項(xiàng)和,求S100 ;
(2)求數(shù)列{an}和{bn}的通項(xiàng)公式.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() 的長(zhǎng)軸為
的長(zhǎng)軸為![]() ,且過點(diǎn)
,且過點(diǎn)![]()
(1)求橢圓![]() 的方程;
的方程;
(2)設(shè)點(diǎn)![]() 為原點(diǎn),若點(diǎn)
為原點(diǎn),若點(diǎn)![]() 在曲線
在曲線![]() 上,點(diǎn)
上,點(diǎn)![]() 在直線
在直線![]() 上,且
上,且![]() ,試判斷直線
,試判斷直線![]() 與圓
與圓![]() 的位置關(guān)系,并證明你的結(jié)論.
的位置關(guān)系,并證明你的結(jié)論.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】對(duì)于函數(shù)![]() ,若在定義域內(nèi)存在實(shí)數(shù)
,若在定義域內(nèi)存在實(shí)數(shù)![]() ,滿足
,滿足![]() ,則稱
,則稱![]() 為“局部奇函數(shù)”.
為“局部奇函數(shù)”.
(1)已知二次函數(shù)![]() ,試判斷
,試判斷![]() 是否為“局部奇函數(shù)”?并說明理由;
是否為“局部奇函數(shù)”?并說明理由;
(2)若![]() 是定義在區(qū)間
是定義在區(qū)間![]() 上的“局部奇函數(shù)”,求實(shí)數(shù)
上的“局部奇函數(shù)”,求實(shí)數(shù)![]() 的取值范圍;
的取值范圍;
(3)若![]() 為定義域
為定義域![]() 上的“局部奇函數(shù)”,求實(shí)數(shù)
上的“局部奇函數(shù)”,求實(shí)數(shù)![]() 的取值范圍;
的取值范圍;
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】《中華人民共和國(guó)個(gè)人所得稅法》規(guī)定,公民月收入總額(工資、薪金等)不超過免征額的部分不必納稅,超過免征額的部分為全月應(yīng)納稅所得額,個(gè)人所得稅稅款按稅率表分段累計(jì)計(jì)算.為了給公民合理減負(fù),穩(wěn)步提升公民的收入水平,自2018年10月1日起,個(gè)人所得稅免征額和稅率進(jìn)行了調(diào)整,調(diào)整前后的個(gè)人所得稅稅率表如下:

(1)已知小李2018年9月份上交的稅費(fèi)是295元,10月份月工資、薪金等稅前收入與9月份相同,請(qǐng)幫小李計(jì)算一下稅率調(diào)整后小李10月份的稅后實(shí)際收入是多少?
(2)某稅務(wù)部門在小李所在公司利用分層抽樣方法抽取某月100位不同層次員工的稅前收入,并制成下面的頻率分布直方圖.
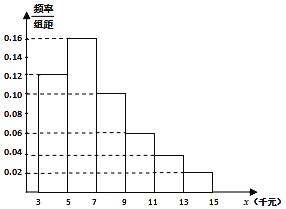
(ⅰ)請(qǐng)根據(jù)頻率分布直方圖估計(jì)該公司員工稅前收入的中位數(shù);
(ⅱ)同一組中的數(shù)據(jù)以這組數(shù)據(jù)所在區(qū)間中點(diǎn)的值作代表,按調(diào)整后稅率表,試估計(jì)小李所在的公司員工該月平均納稅多少元?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() ,若關(guān)于x的方程
,若關(guān)于x的方程![]() 有四個(gè)不等實(shí)根,且
有四個(gè)不等實(shí)根,且![]() 恒成立,則實(shí)數(shù)
恒成立,則實(shí)數(shù)![]() 的最小值為________.
的最小值為________.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() 的左右焦點(diǎn)分別為
的左右焦點(diǎn)分別為![]() ,離心率為
,離心率為![]() ,點(diǎn)
,點(diǎn)![]() 在橢圓
在橢圓![]() 上,且
上,且![]() 的周長(zhǎng)為
的周長(zhǎng)為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)已知過點(diǎn)![]() 的直線與橢圓
的直線與橢圓![]() 交于
交于![]() 兩點(diǎn),點(diǎn)
兩點(diǎn),點(diǎn)![]() 在直線
在直線![]() 上,求
上,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】有次水下考古活動(dòng)中,潛水員需潛入水深為30米的水底進(jìn)行作業(yè),其用氧量包含以下三個(gè)方面:①下潛時(shí),平均速度為每分鐘![]() 米,每分鐘的用氧量為
米,每分鐘的用氧量為![]() 升;②水底作業(yè)需要10分鐘,每分鐘的用氧量為0.3升;③返回水面時(shí),速度為每分鐘
升;②水底作業(yè)需要10分鐘,每分鐘的用氧量為0.3升;③返回水面時(shí),速度為每分鐘![]() 米,每分鐘用氧量為0.2升;設(shè)潛水員在此次考古活動(dòng)中的總用氧量為
米,每分鐘用氧量為0.2升;設(shè)潛水員在此次考古活動(dòng)中的總用氧量為![]() 升;
升;
(1)將![]() 表示為
表示為![]() 的函數(shù);
的函數(shù);
(2)若![]() ,求總用氧量
,求總用氧量![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在平行四邊形ABCD中,![]() ,四邊形ACEF為正方形,且平面
,四邊形ACEF為正方形,且平面![]() 平面ACEF.
平面ACEF.
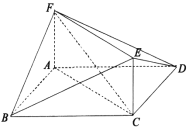
(1)證明:![]() ;
;
(2)求平面BEF與平面BCF所成銳二面角的余弦值.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com