
���}Ŀ����ֱ������![]() �У�
�У�![]() ��������߅�L�քe��3��5��7��
��������߅�L�քe��3��5��7��![]() ���ϵ���
���ϵ���![]() ����ƽ���(n��i)�Ą�(d��ng)�c(di��n)���������F
����ƽ���(n��i)�Ą�(d��ng)�c(di��n)���������F![]() ����������e��
����������e��![]() ���t�M���}��Ą�(d��ng)�c(di��n)
���t�M���}��Ą�(d��ng)�c(di��n)![]() ��܉�E��(du��)��(y��ng)�D�ε���e��________.
��܉�E��(du��)��(y��ng)�D�ε���e��________.
���𰸡�![]()
��������
�O(sh��)![]() ��
��![]() ��ӈA�A�ģ���
��ӈA�A�ģ���![]() ƽ��
ƽ��![]() ������(j��)�����F���������|(zh��)��֪����
������(j��)�����F���������|(zh��)��֪����![]() ��
��![]() ��һ�c(di��n)����
��һ�c(di��n)����![]() �У��Y(ji��)�������Ҷ��������
�У��Y(ji��)�������Ҷ��������![]() ����ӈA�돽���M(j��n)�����ɶ�����������ĵ�ƽ��
����ӈA�돽���M(j��n)�����ɶ�����������ĵ�ƽ��![]() �ľ��x�������ù��ɶ������
�ľ��x�������ù��ɶ������![]() ���ɵ�
���ɵ�![]() �c(di��n)܉�E��A���M(j��n)����ýY(ji��)��.
�c(di��n)܉�E��A���M(j��n)����ýY(ji��)��.
�����O(sh��)![]() ��
��![]() ��
��![]() ��
��
�O(sh��)![]() ��
��![]() ��ӈA�A�ģ���
��ӈA�A�ģ���![]() ƽ��
ƽ��![]() ����ƽ��
����ƽ��![]() ���c(di��n)
���c(di��n)![]() ���������F���������|(zh��)��֪������
���������F���������|(zh��)��֪������![]() ��
��![]() ��һ�c(di��n).
��һ�c(di��n).
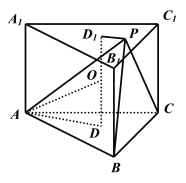
�O(sh��)�����F![]() �����돽��
�����돽��![]() ��
��
![]() �����F
�����F![]() ��������e
��������e![]() ��
��![]() .
.
��![]() �У������Ҷ����ã�
�У������Ҷ����ã�![]() ��
��
![]() �������Ҷ����ã�
�������Ҷ����ã�![]() ��
��
![]() ����
����![]() ��
��![]() ��
��
![]() ��
��
���c(di��n)![]() ��܉�E��(du��)��(y��ng)�ĈD������
��܉�E��(du��)��(y��ng)�ĈD������![]() ��A�ģ�
��A�ģ�![]() ��돽�ĈA��
��돽�ĈA��
![]() ��(du��)��(y��ng)�ĈD����e��
��(du��)��(y��ng)�ĈD����e��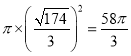 .
.
�ʴ𰸞飺![]() .
.


 ��x��܇ϵ�д�
��x��܇ϵ�д�
| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����D��ʾ�������F![]() �У�
��![]() ��
��![]() ��
��![]() ��
��![]() ���c(di��n)
���c(di��n)![]() �քe��
�քe��![]() �����c(di��n)��
�����c(di��n)��
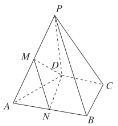
��1���C����ƽ��![]() ��ƽ��
��ƽ��![]() ��
��
��2����![]() ������ֱ��
������ֱ��![]() �c
�c![]() ���ɽǵ�����ֵ��
���ɽǵ�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����D��ʾ����֪�E�A��![]() (
(![]() )���x���ʞ�
)���x���ʞ�![]() ���Ҝ�(zh��n)��������ֱ��l��
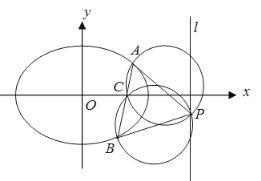
���Ҝ�(zh��n)��������ֱ��l��![]() ���c(di��n)P��ֱ��l�ϵ�һ��(g��)��(d��ng)�c(di��n)���^�c(di��n)P���E�A�ăɗl�о�
���c(di��n)P��ֱ��l�ϵ�һ��(g��)��(d��ng)�c(di��n)���^�c(di��n)P���E�A�ăɗl�о�![]()
![]() �����c(di��n)�քe��AB(�c(di��n)A��x�S�Ϸ����c(di��n)B��x�S�·�).
�����c(di��n)�քe��AB(�c(di��n)A��x�S�Ϸ����c(di��n)B��x�S�·�).
��1����E�A�Ę�(bi��o)��(zh��n)���̣�
��2�������C���քe��![]()
![]() ��ֱ���ăɈA�����^���c(di��n)C��
��ֱ���ăɈA�����^���c(di��n)C��
����![]() ����ֱ��
����ֱ��![]() �ķ���.
�ķ���.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪�E�A![]() ���x���ʞ�
���x���ʞ�![]() �����^�c(di��n)
�����^�c(di��n)![]() .
.
��1����E�AC�ķ��̣�
��2�����c(di��n)A��B��E�AC��������c(di��n)��ֱ��![]() �cx�S�����c(di��n)D���c(di��n)P�ǙE�AC�Ϯ���A��B�Ą�(d��ng)�c(di��n)��ֱ��AP��BP�քe��ֱ��
�cx�S�����c(di��n)D���c(di��n)P�ǙE�AC�Ϯ���A��B�Ą�(d��ng)�c(di��n)��ֱ��AP��BP�քe��ֱ��![]() ��E���ƃ��c(di��n)����(d��ng)�c(di��n)P�ڙE�AC���\(y��n)��(d��ng)�r(sh��)��
��E���ƃ��c(di��n)����(d��ng)�c(di��n)P�ڙE�AC���\(y��n)��(d��ng)�r(sh��)��![]() �Ƿ�鶨ֵ�����ǣ�Ո(q��ng)���ԓ��ֵ�������ǣ�Ո(q��ng)�f������.
�Ƿ�鶨ֵ�����ǣ�Ո(q��ng)���ԓ��ֵ�������ǣ�Ո(q��ng)�f������.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪ij����2018��12��(g��)�µ������c֧����(sh��)��(j��)���۾��D��D��ʾ��
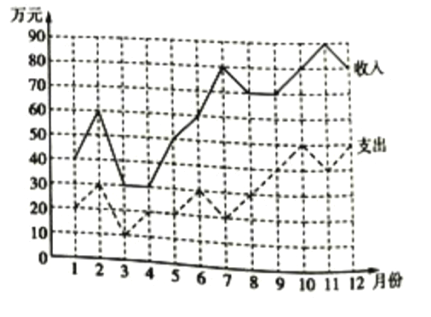
����(j��)ԓ�۾��D��֪�������f���e(cu��)�`���ǣ� ��
A. ԓ����2018���12��(g��)���е�7�·ݵ��������
B. ԓ����2018���12��(g��)���е�4�·ݵ��������
C. ԓ����2018��1-6�·ݵĿ��������2018��7-12�·ݵĿ�����
D. ԓ����2018��7-12�·ݵĿ������2018��1-6�·ݵĿ��������L��90�fԪ
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����ȫ�濹���¹ڷ��������@һ����r(sh��)�ڣ����н����������ͣ�n��ͣ�W(xu��)���Ŀ�̖(h��o)���Ą�(l��)�W(xu��)�����όW(xu��)��(x��).ijУ��(sh��)�W(xu��)�̎������{(di��o)������W(xu��)����(sh��)�W(xu��)�ɿ��c���όW(xu��)��(x��)�r(sh��)�g֮�g�����P(gu��n)�P(gu��n)ϵ����(du��)�����꼉(j��)�S�C(j��)�xȡ45���W(xu��)���M(j��n)�и�ۙ����������ÿ�ܾ��όW(xu��)��(x��)��(sh��)�W(xu��)�r(sh��)�g������5С�r(sh��)����19�ˣ����µ����У��ڙz�y��ԇ�Д�(sh��)�W(xu��)ƽ���ɿ�����120�ֵ�ռ![]() ���y(t��ng)Ӌ(j��)�ɿ���õ�����
���y(t��ng)Ӌ(j��)�ɿ���õ�����![]() ��(li��n)����
��(li��n)����
��?j��n)?sh��)������120�� | ��?j��n)?sh��)����120�� | ��Ӌ(j��) | |
���όW(xu��)��(x��)�r(sh��)�g������5С�r(sh��) | 4 | 19 | |
���όW(xu��)��(x��)�r(sh��)�g����5С�r(sh��) | |||
��Ӌ(j��) | 45 |
��1��Ո(q��ng)�������![]() ��(li��n)�������Д��Ƿ���99%�İ����J(r��n)���������W(xu��)���Ĕ�(sh��)�W(xu��)�ɿ��c�W(xu��)�����όW(xu��)��(x��)�r(sh��)�g���P(gu��n)����
��(li��n)�������Д��Ƿ���99%�İ����J(r��n)���������W(xu��)���Ĕ�(sh��)�W(xu��)�ɿ��c�W(xu��)�����όW(xu��)��(x��)�r(sh��)�g���P(gu��n)����
��2���������ӱ��Џķ�?j��n)?sh��)������120�ֵČW(xu��)���У����շӳ�ӵķ������鵽���όW(xu��)��(x��)�r(sh��)�g������5С�r(sh��)�;��όW(xu��)��(x��)�r(sh��)�g����5С�r(sh��)�ČW(xu��)����5���������@5���W(xu��)�����S�C(j��)��ȡ2�ˣ�������1��ÿ�ܾ��όW(xu��)��(x��)�r(sh��)�g����5С�r(sh��)�ĸ���.
��������R��ֵ����������
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
��������ʽ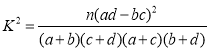 ����
����![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪![]() �ă�(n��i)��
�ă�(n��i)��![]() ����(du��)��߅�քe��
����(du��)��߅�քe��![]() ��_________����
��_________����![]() .�F(xi��n)�ģ���
.�F(xi��n)�ģ���![]() ����
����![]() ����
����![]() �@����(g��)�l�������xһ��(g��)���a(b��)�������φ��}�У����Д��@�ӵ�
�@����(g��)�l�������xһ��(g��)���a(b��)�������φ��}�У����Д��@�ӵ�![]() �Ƿ���ڣ������ڣ���
�Ƿ���ڣ������ڣ���![]() ����e
����e![]() _________���������ڣ�Ո(q��ng)�f������.
_________���������ڣ�Ո(q��ng)�f������.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪�����w![]() ��D��ʾ��
��D��ʾ��![]() ƽ��
ƽ��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ����
����![]() �ϵ��c(di��n)���ҝM��
�ϵ��c(di��n)���ҝM��![]() .
.
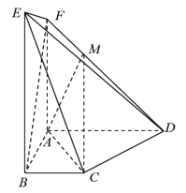
��1�����C��ֱ��![]() ƽ��
ƽ��![]() ��
��
��2��������![]() ������ֵ.
������ֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ������(ji��)�^�ס��ҡ�������Մ?w��)������P(gu��n)![]() ���Ӱ
���Ӱ![]() ��
��![]() ��
��![]() ����r.
����r.
���f���қ]�п��^�Ӱ![]() ��������
��������![]() ���Ӱ�҂�?n��i)���(g��)�����^��
���Ӱ�҂�?n��i)���(g��)�����^��
���f�������Ӱ����![]() ���Ӱ�҂�?n��i)�����ֻ��һ�˿��^��
���Ӱ�҂�?n��i)�����ֻ��һ�˿��^��
���f���Һͼ����Ӱ��![]() ����ͬ����
����ͬ����![]() ����ͬ.
����ͬ.
�����������f������Ԓ���t�ɴ˿��Д������Ӱ���ҿ��^�IJ���(sh��)�ǣ� ��
A.![]() ��B.
��B.![]() ��C.
��C.![]() ��D.
��D.![]() ����
����![]() ��
��
�鿴�𰸺ͽ���>>
���H�W(xu��)У��(y��u)�x - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com