
【題目】已知直線![]() 與橢圓
與橢圓![]() 交于
交于![]() 兩點,且
兩點,且![]() (其中
(其中![]() 為坐標原點),若橢圓的離心率
為坐標原點),若橢圓的離心率![]() 滿足
滿足![]() ,則橢圓長軸的取值范圍是( )
,則橢圓長軸的取值范圍是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】A
【解析】
聯立直線方程與橢圓方程得(a2+b2)x2﹣2a2x+a2﹣a2b2=0,設P(x1,y1),Q(x2,y2),由OP⊥OQ,得![]() =0,由根與系數的關系可得:a2+b2=2a2b2.由橢圓的離心率e滿足
=0,由根與系數的關系可得:a2+b2=2a2b2.由橢圓的離心率e滿足![]() ≤e≤
≤e≤![]() ,化為
,化為![]() ,即可得出.
,即可得出.
聯立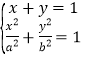 得:(a2+b2)x2﹣2a2x+a2﹣a2b2=0,設P(x1,y1),Q(x2,y2)
得:(a2+b2)x2﹣2a2x+a2﹣a2b2=0,設P(x1,y1),Q(x2,y2)
△=4a4﹣4(a2+b2)(a2﹣a2b2)>0,化為:a2+b2>1.
x1+x2=![]() ,x1x2=
,x1x2=![]() .∵OP⊥OQ,
.∵OP⊥OQ,
∴![]() =x1x2+y1y2=x1x2+(x1﹣1)(x2﹣1)=2x1x2﹣(x1+x2)+1=0,
=x1x2+y1y2=x1x2+(x1﹣1)(x2﹣1)=2x1x2﹣(x1+x2)+1=0,
∴2×![]() ﹣
﹣![]() +1=0.化為a2+b2=2a2b2.∴b2=
+1=0.化為a2+b2=2a2b2.∴b2=![]() .
.
∵橢圓的離心率e滿足![]() ≤e≤
≤e≤![]() ,∴
,∴![]() ,∴
,∴![]() ,
,![]() ,化為5≤4a2≤6.
,化為5≤4a2≤6.
解得:![]() ≤2a≤
≤2a≤![]() .滿足△>0.∴橢圓長軸的取值范圍是[
.滿足△>0.∴橢圓長軸的取值范圍是[![]() ,
,![]() ].
].
故選:A.


科目:高中數學 來源: 題型:
【題目】設![]() ,
,![]() 是兩條不同的直線,
是兩條不同的直線,![]() ,
,![]() ,
,![]() 是三個不同的平面,給出下列四個命題:
是三個不同的平面,給出下列四個命題:
①若![]() ,
,![]() ,則
,則![]()
②若![]() ,
,![]() ,
,![]() ,則
,則![]()
③若![]() ,
,![]() ,則
,則![]()
④若![]() ,
,![]() ,則
,則![]()
其中正確命題的序號是( )
A.①和②B.②和③C.③和④D.①和④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,已知曲線
中,已知曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數).以
為參數).以![]() 為極點,
為極點,![]() 軸正半軸為極軸建立極坐標系,曲線
軸正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求曲線![]() 的極坐標方程和曲線
的極坐標方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)設動直線![]() :
:![]() 分別與曲線
分別與曲線![]() ,
,![]() 相交于點
相交于點![]() ,
,![]() ,求當
,求當![]() 為何值時,
為何值時,![]() 取最大值,并求
取最大值,并求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】以直角坐標系xOy的坐標原點O為極點,x軸的正半軸為極軸建立極坐標系,曲線C1的極坐標方程是![]() ,曲線C2的參數方程是
,曲線C2的參數方程是![]() (θ為參數).
(θ為參數).
(1)寫出曲線C1,C2的普通方程;
(2)設曲線C1與y軸相交于A,B兩點,點P為曲線C2上任一點,求|PA|2+|PB|2的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
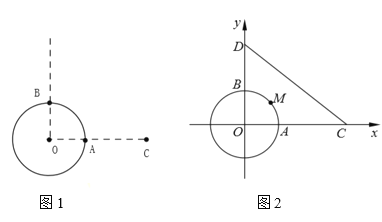
【題目】如圖1,點![]() 為半徑為
為半徑為![]() 千米的圓形海島的最東端,點
千米的圓形海島的最東端,點![]() 為最北端,在點
為最北端,在點![]() 的正東
的正東![]() 千米
千米![]() 處停泊著一艘緝私艇,某刻,發現在
處停泊著一艘緝私艇,某刻,發現在![]() 處有一小船正以速度
處有一小船正以速度![]() (千米/小時)向正北方向行駛,已知緝私艇的速度為
(千米/小時)向正北方向行駛,已知緝私艇的速度為![]() (千米/小時) .
(千米/小時) .
(1)為了在最短的時間內攔截小船檢查,緝私艇應向什么方向行駛? (精確到![]() )
)
(2)海島上有一快艇要為緝私艇送去給養,問選擇海島邊緣的哪一點![]() 出發才能行程最短? (如圖2建立坐標系, 用坐標表示點
出發才能行程最短? (如圖2建立坐標系, 用坐標表示點![]() 的位置)
的位置)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某廠銷售部以箱為單位銷售某種零件,每箱的定價為![]() 元,低于
元,低于![]() 箱按原價銷售,不低于
箱按原價銷售,不低于![]() 箱則有以下兩種優惠方案:①以
箱則有以下兩種優惠方案:①以![]() 箱為基準,每多
箱為基準,每多![]() 箱送
箱送![]() 箱;②通過雙方議價,買方能以優惠
箱;②通過雙方議價,買方能以優惠![]() 成交的概率為
成交的概率為![]() ,以優惠
,以優惠![]() 成交的概率為
成交的概率為![]() .
.
![]() 甲、乙兩單位都要在該廠購買
甲、乙兩單位都要在該廠購買![]() 箱這種零件,兩單位都選擇方案②,且各自達成的成交價格相互獨立,求甲單位優惠比例不低于乙單位優惠比例的概率;
箱這種零件,兩單位都選擇方案②,且各自達成的成交價格相互獨立,求甲單位優惠比例不低于乙單位優惠比例的概率;
![]() 某單位需要這種零件
某單位需要這種零件![]() 箱,以購買總價的數學期望為決策依據,試問該單位選擇哪種優惠方案更劃算?
箱,以購買總價的數學期望為決策依據,試問該單位選擇哪種優惠方案更劃算?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,一個正![]() 和一個平行四邊形ABDE在同一個平面內,其中
和一個平行四邊形ABDE在同一個平面內,其中![]() ,
,![]() ,AB,DE的中點分別為F,G.現沿直線AB將
,AB,DE的中點分別為F,G.現沿直線AB將![]() 翻折成
翻折成![]() ,使二面角
,使二面角![]() 為
為![]() ,設CE中點為H.
,設CE中點為H.
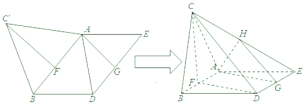
(1)(i)求證:平面![]() 平面AGH;
平面AGH;
(ii)求異面直線AB與CE所成角的正切值;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com