
【題目】如果對于函數f(x)定義域內任意的兩個自變量的值x1 , x2 , 當x1<x2時,都有f(x1)≤f(x2),且存在兩個不相等的自變量值y1 , y2 , 使得f(y1)=f(y2),就稱f(x)為定義域上的不嚴格的增函數.
則 ① , ②
, ② ,
,
③ , ④
, ④![]() ,
,
四個函數中為不嚴格增函數的是 ,若已知函數g(x)的定義域、值域分別為A、B,A={1,2,3},BA,且g(x)為定義域A上的不嚴格的增函數,那么這樣的g(x)有 個.
【答案】①③;9
【解析】解:由已知中:函數f(x)定義域內任意的兩個自變量的值x1 , x2 ,
當x1<x2時,都有f(x1)≤f(x2),
且存在兩個不相等的自變量值y1 , y2 , 使得f(y1)=f(y2),
就稱f(x)為定義域上的不嚴格的增函數.
① , 滿足條件,為定義在R上的不嚴格的增函數;
, 滿足條件,為定義在R上的不嚴格的增函數;
② , 當x1=﹣
, 當x1=﹣![]() , x2∈(﹣
, x2∈(﹣![]() ,
, ![]() ),f(x1)>f(x2),故不是不嚴格的增函數;
),f(x1)>f(x2),故不是不嚴格的增函數;
③ , 滿足條件,為定義在R上的不嚴格的增函數;
, 滿足條件,為定義在R上的不嚴格的增函數;
④![]() , 當x1=
, 當x1=![]() , x2∈(1,
, x2∈(1,![]() ),f(x1)>f(x2),故不是不嚴格的增函數;
),f(x1)>f(x2),故不是不嚴格的增函數;
故已知的四個函數中為不嚴格增函數的是①③;
∵函數g(x)的定義域、值域分別為A、B,A={1,2,3},BA,且g(x)為定義域A上的不嚴格的增函數,
則滿足條件的函數g(x)有:
g(1)=g(2)=g(3)=1,
g(1)=g(2)=g(3)=2,
g(1)=g(2)=g(3)=3,
g(1)=g(2)=1,g(3)=2,
g(1)=g(2)=1,g(3)=3,
g(1)=g(2)=2,g(3)=3,
g(1)=1,g(2)=g(3)=2,
g(1)=1,g(2)=g(3)=3,
g(1)=2,g(2)=g(3)=3,
故這樣的函數共有9個,
所以答案是:①③;9.


 教學練新同步練習系列答案
教學練新同步練習系列答案 課前課后同步練習系列答案
課前課后同步練習系列答案科目:高中數學 來源: 題型:
【題目】已知橢圓C: ![]() =1(a>b>0)的短軸一個端點到右焦點F的距離為2,且過點
=1(a>b>0)的短軸一個端點到右焦點F的距離為2,且過點 ![]() .
.
(1)求橢圓C的方程;
(2)設M,N為橢圓C上不同的兩點,A,B分別為橢圓C上的左右頂點,直線MN既不平行與坐標軸,也不過橢圓C的右焦點F,若∠AFM=∠BFN,求證:直線MN過定點.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在多面體![]() 中,平面
中,平面![]() 平面
平面![]() ,四邊形
,四邊形![]() 為正方形,四邊形
為正方形,四邊形![]() 為梯形,且
為梯形,且![]() ,
,![]() ,
,![]() .
.

(Ⅰ)求證:![]() 平面
平面![]() ;
;
(Ⅱ)求證:![]() 平面
平面![]() ;
;
(Ⅲ)在線段![]() 上是否存在點
上是否存在點![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】現在,很多人都喜歡騎“共享單車”,但也有很多市民并不認可.為了調查人們對這種交通方式的認可度,某同學從交通擁堵不嚴重的A城市和交通擁堵嚴重的B城市分別隨機調查了20名市民,得到了一個市民是否認可的樣本,具體數據如下![]() 列聯表:
列聯表:
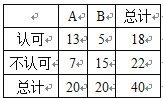
附:![]() ,
,![]() .
.

根據表中的數據,下列說法中,正確的是( )
A. 沒有95% 以上的把握認為“是否認可與城市的擁堵情況有關”
B. 有99% 以上的把握認為“是否認可與城市的擁堵情況有關”
C. 可以在犯錯誤的概率不超過0.01的前提下認為“是否認可與城市的擁堵情況有關”
D. 可以在犯錯誤的概率不超過0.025的前提下認為“是否認可與城市的擁堵情況有關”
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,已知直線
中,已知直線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數).以坐標原點
為參數).以坐標原點![]() 為極點,以坐標原點
為極點,以坐標原點![]() 為極點,
為極點,![]() 軸的非負半軸為極軸,取相同的長度單位建立極坐標系,曲線
軸的非負半軸為極軸,取相同的長度單位建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(Ⅰ)求直線![]() 的普通方程和曲線
的普通方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(Ⅱ)若曲線![]() 上的點到直線
上的點到直線![]() 的最大距離為6,求實數
的最大距離為6,求實數![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某研究機構為了調研當代中國高中生的平均年齡,從各地多所高中隨機抽取了40名學生進行年齡統計,得到結果如下表所示:
年齡(歲) |
|
|
|
|
|
數量 | 6 | 10 | 12 | 8 | 4 |
(Ⅰ)若同一組數據用該組區間的中點值代表,試估計這批學生的平均年齡;
(Ⅱ)若在本次抽出的學生中隨機挑選2人,記年齡在![]() 間的學生人數為
間的學生人數為![]() ,求
,求![]() 的分布列及數學期望.
的分布列及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 是菱形,對角線
是菱形,對角線![]() ,
,![]() 交于點
交于點![]() .
.

(Ⅰ)若![]() ,求證:
,求證:![]() 平面
平面![]() ;
;
(Ⅱ)若平面![]() 平面
平面![]() ,求證:
,求證:![]() ;
;
(Ⅲ)在棱![]() 上是否存在點
上是否存在點![]() (異于點
(異于點![]() ),使得
),使得![]() 平面
平面![]() ?說明理由.
?說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《史記》卷六十五《孫子吳起列傳第五》中有這樣一道題:齊王與田忌賽馬,田忌的上等馬優于齊王的中等馬,劣于齊王的上等馬,田忌的中等馬優于齊王的下等馬,劣于齊王的中等馬,田忌的下等馬劣于齊王的下等馬,現從雙方的馬匹中隨機選一匹馬進行一場比賽,齊王獲勝的概率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】從某企業生產的某種產品中抽取![]() 件,測量這些產品的一項質量指標值,由測量結果得如頻率分布直方圖:
件,測量這些產品的一項質量指標值,由測量結果得如頻率分布直方圖:
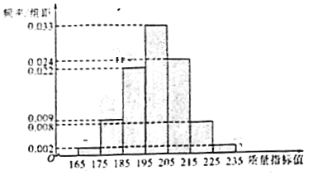
(1)求這![]() 件產品質量指標值的樣本平均數
件產品質量指標值的樣本平均數![]() 和樣本方差
和樣本方差![]() (同一組中的數據用該組區間的中點值作代表);
(同一組中的數據用該組區間的中點值作代表);
(2)由直方圖可以認為,這種產品的質量指標值![]() 服從正態分布
服從正態分布![]() ,其中
,其中![]() 近似為樣本平均數
近似為樣本平均數![]() ,
,![]() 近似為樣本方差
近似為樣本方差![]() .
.
①利用該正態分布,求![]() ;
;
②某用戶從該企業購買了![]() 件這種產品,記
件這種產品,記![]() 表示這
表示這![]() 件產品中質量指標值位于區間
件產品中質量指標值位于區間![]() 的產品件數.利用①的結果,求
的產品件數.利用①的結果,求![]() .
.
附:![]() .若
.若![]() ,則
,則![]() ,
,![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com