
【題目】設函數f(x)的導函數為f′(x),若f(x)=![]() ex﹣f(0)x+
ex﹣f(0)x+![]() x2(e是自然對數的底數).
x2(e是自然對數的底數).
(1)求f(0)和f′(1)的值;
(2)若g(x)=![]() x2+a與函數f(x)的圖象在區間[﹣1,2]上恰有2兩個不同的交點,求實數a的取值范圍.
x2+a與函數f(x)的圖象在區間[﹣1,2]上恰有2兩個不同的交點,求實數a的取值范圍.
【答案】解:(1)∵f(x)=![]() ex﹣f(0)x+
ex﹣f(0)x+![]() x2 ,
x2 ,
∴f′(x)=![]() ex﹣f(0)+x,
ex﹣f(0)+x,
∴f′(1)=f′(1)﹣f(0)+1,
∴f(0)=1,
∴f(x)=![]() ex﹣x+
ex﹣x+![]() x2 ,
x2 ,
∴f(0)=f′(1)﹣0+0,
∴f′(1)=1.
(2)由(1)可得:f(x)=![]() ﹣x+
﹣x+![]() x2 ,
x2 ,
由g(x)=![]() x2+a=f(x),化為a=
x2+a=f(x),化為a=![]() ﹣x=h(x),x∈[﹣1,2].
﹣x=h(x),x∈[﹣1,2].
∴h′(x)=![]() =
=![]() ,
,
令h′(x)>0,解得1<x<2,此時函數h(x)單調遞增;令h′(x)<0,解得﹣1<x<1,此時函數h(x)單調遞減.
∴當x=1時,函數h(x)取得最小值,h(1)=0.而h(﹣1)=![]() ,h(2)=e﹣2.
,h(2)=e﹣2.
∵g(x)=![]() x2+a與函數f(x)的圖象在區間[﹣1,2]上恰有2兩個不同的交點,
x2+a與函數f(x)的圖象在區間[﹣1,2]上恰有2兩個不同的交點,
∴0<a<e﹣2.
∴實數a的取值范圍是(0,e﹣2).
【解析】(1)由f(x)=![]() ex﹣f(0)x+
ex﹣f(0)x+![]() x2 , 可得f′(x)=
x2 , 可得f′(x)=![]() ex﹣f(0)+x,令x=1,可得f(0),進而得到f′(1).
ex﹣f(0)+x,令x=1,可得f(0),進而得到f′(1).
(2)g(x)=![]() x2+a與函數f(x)的圖象在區間[﹣1,2]上恰有2兩個不同的交點y=a與h(x)=
x2+a與函數f(x)的圖象在區間[﹣1,2]上恰有2兩個不同的交點y=a與h(x)=![]() ﹣x在x∈[﹣1,2]上有兩個不同交點.利用導數研究函數h(x)的單調性極值與最值,結合圖象即可得出.
﹣x在x∈[﹣1,2]上有兩個不同交點.利用導數研究函數h(x)的單調性極值與最值,結合圖象即可得出.


 字詞句篇與同步作文達標系列答案
字詞句篇與同步作文達標系列答案科目:高中數學 來源: 題型:
【題目】空氣質量指數AQI是反映空氣質量狀況的指數,AQI指數值越小,表明空氣質量越好,其對應關系如下表:
AQI指數值 | 0~50 | 51~100 | 101~150 | 151~200 | 201~300 | >300 |
空氣質量 | 優 | 良 | 輕度污染 | 中度污染 | 重度污染 | 嚴重污染 |
下圖是某市10月1日—20日AQI指數變化趨勢:

下列敘述錯誤的是
A. 這20天中AQI指數值的中位數略高于100
B. 這20天中的中度污染及以上的天數占![]()
C. 該市10月的前半個月的空氣質量越來越好
D. 總體來說,該市10月上旬的空氣質量比中旬的空氣質量好
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某中學將100名高一新生分成水平相同的甲、乙兩個“平行班”,每班50人.陳老師采用A,B兩種不同的教學方式分別在甲、乙兩個班級進行教改實驗.為了解教學效果,期末考試后,陳老師分別從兩個班級中各隨機抽取20名學生的成績進行統計,作出莖葉圖如圖.記成績不低于90分者為“成績優秀”.

(1)在乙班樣本的20個個體中,從不低于86分的成績中隨機抽取2個,求抽出的2個均“成績優秀”的概率;
(2)由以上統計數據作出列聯表,并判斷能否在犯錯誤的概率不超過0.1的前提下認為:“成績優秀”與教學方式有關.
| 0.400 | 0.250 | 0.150 | 0.100 | 0.050 | 0.025 |
| 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
參考公式:![]()
![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,
中,![]() 平面
平面![]() ,在直角梯形
,在直角梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 為線段
為線段![]() 的中點
的中點
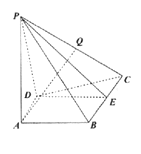
(1)求證:平面![]() 平面
平面![]()
(2)在線段![]() 上是否存在點
上是否存在點![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求出點
?若存在,求出點![]() 的位置;若不存在,請說明理由
的位置;若不存在,請說明理由
(3)若![]() 是
是![]() 中點,
中點,![]() ,
,![]() ,
,![]() ,求三棱錐
,求三棱錐![]() 的體積.
的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,四棱錐![]() 中,底面
中,底面![]() 為平行四邊形,
為平行四邊形, ![]() 底面
底面![]() ,
, ![]() 是棱
是棱![]() 的中點,
的中點,
且![]() .
.

(1)求證: ![]() 平面
平面![]() ;
;
(2)如果![]() 是棱
是棱![]() 上一點,且直線
上一點,且直線![]() 與平面
與平面![]() 所成角的正弦值為
所成角的正弦值為![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com